- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2005
- Surface and Interface Science
- Site-specific Valence Band Structure of SrTiO<sub>3</sub> Determined by X-ray Standing Waves
Site-specific Valence Band Structure of SrTiO<sub>3</sub> Determined by X-ray Standing Waves
Structure and chemical composition define the properties of materials, notably the band structure, i.e., the valence band and conduction band, of solids. The band structure in turn is predominantly responsible for the optical and electronic characteristics of a material, such as the colour and the ability to reflect or absorb light or the electrical conductivity and the speed of electronic transport. Using X-ray photoelectron spectroscopy (XPS), a well-known tool for studying the chemical composition of materials, and combining it with the X-ray standing wave (XSW) technique, we can obtain electronic information on the atomic scale. It is possible to revealing how structure and chemical composition are related to the electronic structure of a solid. We used this method at ID32 to accurately determine the site within the unit cell of a SrTiO3 crystal from which the electrons from a specific region of the valence band originate. SrTiO3 is a wide gap (3.2 eV) semiconductor with a cubic structure where titanium occupies the centre and strontium the corners of the cube, while oxygen resides at the centre of the six faces. The unit cell, shown in Figure 99, has a side length of 0.3905 nm.
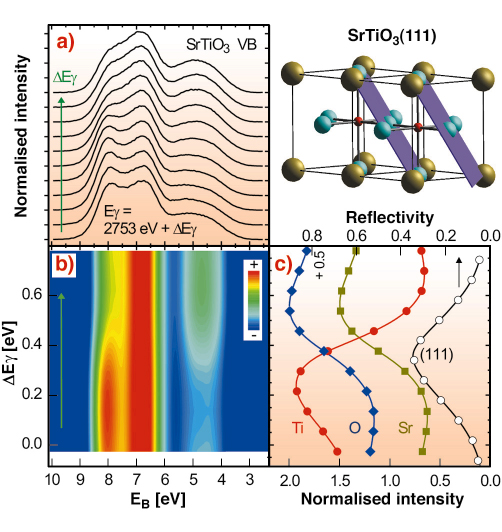 |
|
Fig. 99: Two SrTiO3 unit cells, with the (111) standing wave planes indicated, are shown in the top right hand part. Oxygen atoms are in blue, titanium in red and strontium atoms in olive. a) SrTiO3 valence band for different standing wave positions while crossing the (111) reflection. b) 2D colour rendering of a). c) SrTiO3(111) reflection curve and simultaneously recorded Ti, O, and Sr core levels. 2.753 keV is the energy at which the (111) reflection would occur according to Braggs law. |
An XSW can be generated by interference via Bragg reflecting an X-ray plane wave from a single crystal. The period of this interference field reflects the spacing of the diffracting planes, which are indicated with respect to the SrTiO3 unit cell for a (111) reflection in Figure 99. We can shift this wavefield by varying the X-ray energy within the range of the Bragg reflection, which occurs over a few 100 meV. In this way we can scan the planes of the interference field in a controlled way across the atomic positions. A maximum number of photoelectrons with a characteristic energy will be emitted when the maxima of the wavefield coincide with the centre of the atoms of a specific element in the unit cell, here Sr, Ti, and O. The emission will be strongly localised even for the largely delocalised valence band electrons, since the dipole approximation applies, meaning that photoelectron emission occurs exclusively from the centre of the atoms.
The results of an XSW/XPS measurement, using a (111) reflection from a (001) oriented SrTiO3 crystal in backreflection at around 2.753 keV are shown in Figure 99. The valence band recorded for different positions of the standing wave within the unit cell exhibits a pronounced variation in line shape, as shown in Figure 99a and 99b. Figure 99c shows the simultaneously recorded reflectivity curve, which allows unambiguous determination of the position of the wavefield within the unit cell of the SrTiO3 crystal, and at the same time records core levels from O, Sr, and Ti. A maximum in the core emission is observed when the maxima of the wavefield are located at the position of the corresponding atoms. From a visible inspection of Figure 99a,b and comparison with Figure 99c one can conclude that the valence band at about 4.5 eV binding energy EB is dominated by emission from Sr- and O-sites whereas at EB = 8 eV the photoelectrons are mostly originating from Ti-sites. With respect to the (111) reflection, Sr and Ti are located on a common plane. However, utilising another suitable Bragg reflection, the contribution from the Sr and O-sites can be disentangled.
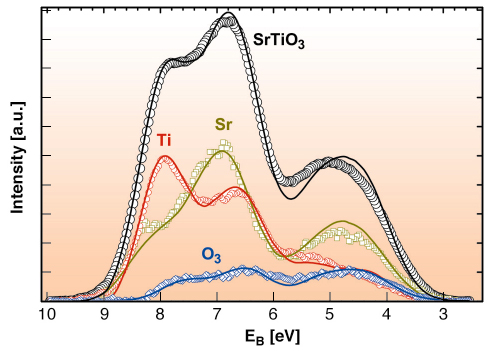 |
|
Fig. 100: SrTiO3 valence band and the determined partial contribution to the valence band from the titanium, oxygen and strontium sites. The overall energy resolution is 750 meV. Symbols: experimental results; lines: DFT/LDA calculations, weighted with cross sections. |
The result of a quantitative XSW analysis is shown in Figure 100 compared with the results of ab initio density functional theory (DFT) calculations in the local density approximation (LDA). The agreement is excellent. It should be noted that the density of states, which are determined by theory, must be weighted for comparison with the experimentally obtained XPS spectra. This must be carried out for the individual elements and angular momentum states. These a priori unknown values for the solid state, valence band cross sections are a further important result of this study.
Authors
S. Thiess (a), T-L. Lee (a), F. Bottin (b), J. Zegenhagen (a).
(a) ESRF
(b) CEA/DIF, Bruyeres-le-Chatel (France)



