- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2005
- High Resolution and Resonance Scattering
- Non-ergodicity in Locally-ordered Systems in the Proximity of the Glass Transition
Non-ergodicity in Locally-ordered Systems in the Proximity of the Glass Transition
When a simple liquid is cooled below its melting temperature, each particle becomes trapped progressively in the transient cage formed by its nearest neighbours, and partakes in correlated collisions inducing a strong damping of the motion. Successive diffusion out of the cage needs a cooperative rearrangement of many particles and provides long-range transport motion, which lessens drastically as the temperature is lowered. This cage effect mechanism can be regarded as the microscopic origin of the eventual structural arrest of the liquid occurring at the glass-transition. In more complex systems like associated and covalent liquids, the ubiquitous class of liquids including water and silica, the cage effect manifests a different nature since molecules are trapped in energetic cages of hydrogen or covalent bonds, and bond breaking and formation is needed for diffusion to occur. Finding a common paradigm to explain the structural arrest in the different classes of liquids represents an important challenge for condensed matter physics.
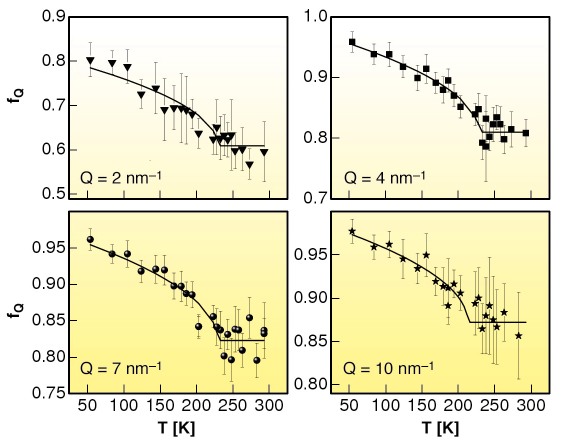
The mode coupling theory (MCT) was introduced to give a self-consistent description of the density-fluctuation dynamics and of the particle caging in liquids [1]. The derived equations of motion for the density-fluctuations lead to a bifurcation of the long-time limit of the density correlators, the so-called non ergodicity factor fQ, if a control parameter like temperature crosses a critical value, Tc. Within MCT, specific predictions are advanced for the temperature and wave vector dependence of f(Q,T): i) A square-root temperature behaviour below Tc, i.e., fQ(T) = fQc + hQ ![]() Tc– T/Tc , where fQc is the critical non-ergodicity parameter and hQ the critical amplitude at a fixed wavevector Q; ii) A Q-dependence of fQc and of hQ that follows the oscillations of the static structure factor S(Q).
Tc– T/Tc , where fQc is the critical non-ergodicity parameter and hQ the critical amplitude at a fixed wavevector Q; ii) A Q-dependence of fQc and of hQ that follows the oscillations of the static structure factor S(Q).
While a large number of experimental and theoretical studies have been devoted to the verification of the MCT predictions in Van-der-Waals molecular liquids, not as much attention has been devoted to associated and covalent liquids, and the results are often mutually conflicting. In these liquids, the local order extends over several neighbouring molecules reflecting a non-trivial Q behaviour in the low-Q region of the static structure factor, S(Q). This Q regime has only recently been made accessible to experimental investigations thanks to development of the high-resolution inelastic X-ray scattering (IXS) technique.
The molecular system of interest here, m-toluidine, is characterised by a spatial organisation of the molecules induced by hydrogen bonds extending over several molecular diameters and giving rise to nanometre-size clusters [2]. The non-ergodicity factor of supercooled and glassy m-toluidine has been measured, through IXS experiments performed at beamline ID16, in the mesoscopic Q range between 1 and 10 nm-1, around the prepeak in the static structure factor related to the local order (Qpp = 5 nm-1).
 |
|
Fig. 18: Temperature dependence of the non-ergodicity factor fQ of m-toluidine for different values of the exchanged wavevector Q. The solid lines are the best fits obtained using the square-root function predicted by the MCT. |
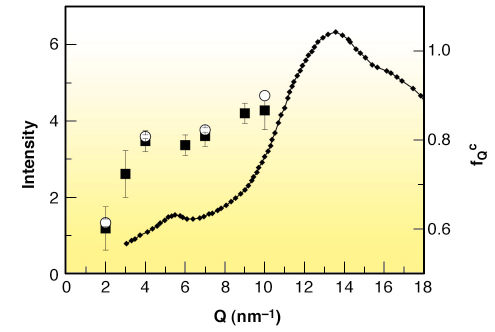
We show that the basic general predictions of MCT about the non-ergodicity factor are verified in m-toluidine (see Figure 18 and Figure 19), providing experimental evidence that the signature of the ergodic to non-ergodic transition, valid for simple liquids, lives on in clustering systems. The present findings indicate that the early stage of the cooperative rearrangements, where the cage effect dominates the molecular dynamics, exhibits a universal character, common to simple liquids and liquids with a local order. This generality is not so obvious, because it puts on the same level the structural arrest in simple and in locally ordered liquids, notwithstanding that cage formation is controlled by different mechanisms. This picture opens the way to the investigation of the fast dynamics of a wider class of clustering systems, including network forming polymers, where the structural arrest is controlled by irreversible bond formation.
 |
|
Fig. 19: X-ray diffraction pattern (left axis) of liquid m-toluidine at ambient temperature taken from Ref. [2], compared with the parameter fQc (right axis) obtained from the fit of the experimental fQ(T) data (open circles); full squares indicate the values of fQ at T = 263 K — a temperature in the plateau region of fQ(T) — for all the available Q. |
References
[1] W. Götze, and L. Sjögren, Rep. Prog. Phys., 55, 241 (1992).
[2] D. Morineau et al., Europhys. Lett., 43, 195 (1998); M. Descamps et al., Prog. Theor. Phys. Suppl. 126, 207 (1997).
Principal Publication and Authors
L. Comez (a,b,c), S. Corezzi (a,b,d), G. Monaco (e), R. Verbeni (e), and D. Fioretto (a,b,c), Phys. Rev. Lett., 94, 155702 (2005).
(a) INFM CRS-SOFT, c/o Universita´ di Roma ‘‘La Sapienza’’, (Italy)
(b) INFM UdR-PG, c/o Dipartimento di Fisica, Universita´ di Perugia (Italy)
(c) Dipartimento di Fisica, Universita´ di Perugia, (Italy)
(d) Dipartimento di Fisica, Universita´ di Roma ‘‘La Sapienza’’ (Italy)
(e) ESRF



