- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2004
- X-ray Absorption and Magnetic Scattering
- Cu L4 edge Resonant Inelastic X-ray Scattering Sheds Light on dd Excitations of Cuprates
Cu L4 edge Resonant Inelastic X-ray Scattering Sheds Light on dd Excitations of Cuprates
Resonant Inelastic X-ray Scattering (RIXS) can be effectively used to study the low energy electronic and magnetic excitations in solids. Working at the L2,3 absorption edges is ideal in 3d transition metals compounds, because the resonant excitation and de-excitation allow us to measure the energy of excited states unreachable by direct electric dipole transitions. Those excited states (among them the so-called dd excitations, which are transitions within the 3d states that leave unchanged the number of d electrons) extend from a few eV's down to the tens of millielectronvolt energy scale. As the 2p state binding energies of 3d transition metals are between 400 eV and 1000 eV, the L2,3 absorption edges fall in the energetic range of beamline ID08.
To record good RIXS spectra, a high resolving power is needed both in the monochromator (before the sample) and in the spectrometer (after the sample). This is challenging as RIXS is intrinsically a very low count rate experiment, requiring a high flux in a small portion of the sample. At ID08, RIXS has been measured for more than 10 years thanks to the AXES spectrometer and to PoLIFEMo, a dedicated monochromator (both are property of INFM-CNR, designed and developed at the Politecnico di Milano). After the recent upgrade of the whole instrumentation we can now reach a combined resolving power of 2000 (recently measured at the Mn L3 edge, 640 eV). The first use of the new remarkable performance of AXES has been the study of the dd excitations in the cuprates.
Cuprates are a family of Cu based oxides with layered crystalline structure. They are widely studied for their intriguing electronic and magnetic properties, leading in some cases to superconductivity at a remarkably high temperature. The Cu ions are nominally divalent in all cases: the 3d9 configuration is thus characterised by one hole in the 3d states. In all layered cuprates (and practically in CuO as well) every Cu atom is surrounded by four O atoms in a planar 90° coordination (see inset in Figure 128), whereas the out of plane coordination varies. In all cases the in-plane oxygens are the Cu nearest neighbours, forcing the 3d hole to have the x2-y2 symmetry proper of the Cu local coordination. The dd excitations correspond to a change of the symmetry of the Cu hole from x2-y2 to a different one compatible with the local crystalline symmetry, whereas the charge-transfer excitations correspond to the transfer of the Cu 3d hole to those states with dominant O 2p character. The RIXS process can be summarised as (3d)9 ![]() (2p3/2)3
(2p3/2)3 ![]() [(3d)9*;(3d)10L]: the RIXS spectral distribution gives a direct image of the various excitations (we indicated the dd and the charge transfer excitations by the (3d)9* and (3d)10L notation respectively).
[(3d)9*;(3d)10L]: the RIXS spectral distribution gives a direct image of the various excitations (we indicated the dd and the charge transfer excitations by the (3d)9* and (3d)10L notation respectively).
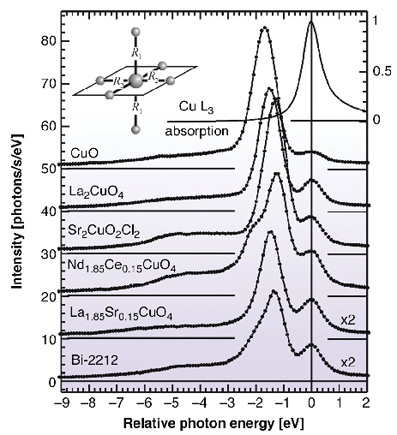 |
Fig. 128: The RIXS spectra measured at the Cu L3 peak from three insulating and three superconducting cuprates. The topmost curve shows the Cu L1.85 absorption peak of La3Sr0.15CuO4. Inset: the local D4h crystal field symmetry used in the calculations. |
In Figure 128 we compare the RIXS spectra of a variety of compounds. The peak at zero relative scattered photon energy is the elastic peak: the system returns to the ground state after the scattering. The main intensity between 1 eV and and 2.5 eV corresponds to the dd excitations. Between 2 eV and 7 eV we can find the charge transfer excitations. It is evident that the dd excitation peak has different shape and position in the various materials, as a direct consequence of the different out-of-plane coordination of the Cu ion. As a rule of thumb, a weaker electrostatic apical perturbation (for example due to a longer distance of the apical oxygen) corresponds to a higher average energy of the dd excitations. This trend is clearly visible in Figure 129, where we compare CuO, having no apical oxygens, with La2CuO4, having a tetragonally distorted octahedral coordination. Relatively simple calculations (atomic model, with point charge crystal field) are also shown. The calculations are in fair agreement with the experiment, providing a strong support to the general interpretation given above within a crystal field model.
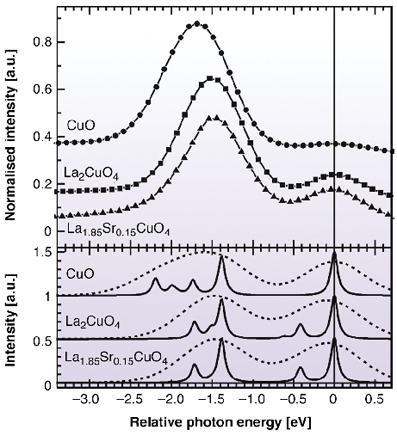 |
Fig. 129: Upper panel: measured RIXS spectra for CuO, La2CuO4, and La1.85Sr0.15CuO4. Bottom panel: calculated RIXS spectra in D4h crystal field symmetry. The spectra are given with a 0.05 eV Lorentzian broadening in the final state (solid lines) and after a 0.8 eV Gaussian broadening (dashed lines). |
We have shown that high resolution and high quality RIXS at the L3 edge of Cu is an effective tool to study the local symmetry of the electronic 3d population. This method can be applied to all the 3d transition metal compounds and to the rare earth systems.
Principal Publications and Authors
G. Ghiringhelli (a), N.B. Brookes (b), E. Annese (c), H. Berger (d), C. Dallera (a), M. Grioni (d), L. Perfetti (d), A. Tagliaferri (a), and L. Braicovich (a), Physical Review Letters 92, 117406 (2004).
(a) INFM-CNR and Dipartimento di Fisica, Politecnico di Milano (Italy)
(b) ESRF
(c) INFM-CNR and Dipartimento di Fisica, Università di Modena e Reggio Emilia (Italy)
(d) Ecole Polytechnique Fédérale de Lausanne (Switzerland)



