- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2004
- X-ray Absorption and Magnetic Scattering
- Direct Observation of Orbital Magnetism in Cubic Solids
Direct Observation of Orbital Magnetism in Cubic Solids
The magnetic moment of the 3d transition metals consists of two contributions: the spin moment µs and the orbital moment µl. Theoretically it is often sufficient to treat the spin-orbit-coupling (SOC) as a weak perturbation. However, strictly speaking magnetism is a relativistic effect and may require a fully relativistic treatment. In principle, l and s are not good quantum numbers, whereas j is. An enormous amount of literature discusses the magnetic phenomena in terms of spin magnetism. However, from a certain point of view the orbital magnetism may be even more important: a finite orbital momentum l is an indication of a non-spherical charge distribution be it for an atom or in solids. Such a non-spherical charge distribution is the primary source for the magnetic anisotropy energy, which is an important quantity e.g. for the fabrication of hard or soft magnets. Nowadays the investigation of 3d transition metal clusters on surfaces has become very important in view of magnetic nanotechnology. "Giant magnetic anisotropy" has recently been reported [1]. Several groups have shown that on surfaces or in nanoclusters one observes giant orbital magnetic moments and magnetic anisotropy energies, respectively, confirming an old theory by L. Néel that the symmetry breaking at surfaces keeps the orbital momentum "alive". For 3d elements in three-dimensional bulk materials the opposite limit seems to hold: the research in the 1970's and 1980's on dilute alloys [2]focused mostly on the spin magnetism, e.g. the Kondo Hamiltonian ( JS ![]()
![]() ). This is in agreement with a standard exercise in solid state physics showing that the expectation value of Lz vanishes in cubic symmetry (<Lz> = 0). Prototype cases in experiment and theory were e.g. Mn, Fe, and Co impurities in cubic Cu, Ag, and Au host materials.
). This is in agreement with a standard exercise in solid state physics showing that the expectation value of Lz vanishes in cubic symmetry (<Lz> = 0). Prototype cases in experiment and theory were e.g. Mn, Fe, and Co impurities in cubic Cu, Ag, and Au host materials.
 |
|
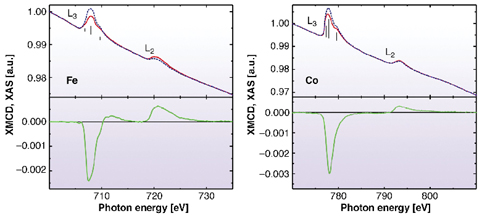
Fig. 117: XAS (upper plots) for left and right circular polarisation and XMCD spectra (lower plots) of ~1at.% Fe and Co in Au at the L2,3 edges. Note the strongly reduced relative intensity at the L2 edge of Co, indicating its enhanced orbital moment. |
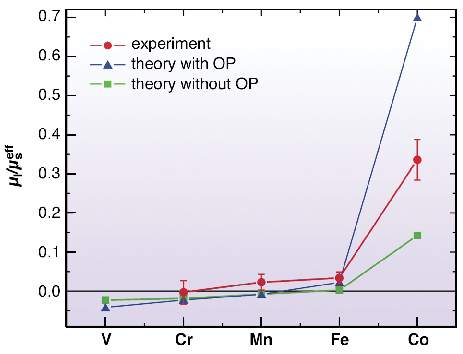
The present work shows that under certain conditions orbital magnetism survives even in a cubic symmetry. X-ray magnetic circular dichroism (XMCD) at the L2,3 edges is an excellent tool to study the ratio µl/µs. Plenty of evidence exists from hyperfine interaction measurements that the orbital magnetism may survive in cubic structures. However, only the third-generation synchrotron facilities have made it possible to measure µs and µl in a direct way. A very high sensitivity is needed because dilute alloys with ~1% impurities correspond to 1/10 monolayer of atoms on a surface. Moreover, a large magnetic field and low temperatures are required to measure dilute paramagnets. These facilities are provided by beamline ID8. Figure 117 shows the normalised X-ray absorption spectra (XAS) of Fe and Co impurities and the corresponding XMCD spectra. The spectra were measured in an external field of 7 Tesla, at temperatures down to 4 K, with normal incidence X-rays. A complete analysis via the sum rules [3] was applied to determine the ratio µl/µs. Here we use a simplified reasoning: For spin magnetism only, theory predicts a 1:1 ratio for the integrated XMCD areas at the L3 and the L2 edge. If the experimental ratio differs from this (obviously for Co) a finite orbital moment survives. The experimental numbers are given in Figure 118 (circles). The experiments find that µl/µs is almost zero for Cr, Mn, and Fe in Au, but 33% for Co/Au.
 |
|
Fig. 118: Comparison of theory and experiment: Systematics of the ratio µl/µs of the 3d series as impurities in Au. |
How can this be understood? Is this in conflict with the quenching of orbital momentum in cubic symmetry? Some insight is given by ab initio calculations (Figure 118, triangles and squares). The calculations also yield a vanishing ratio for all the 3d elements except Co. Two values for µl/µs are given: 15 % and 70 %. The lower value was calculated in a scalar relativistic approach including spin-orbit-coupling only as a weak perturbation (Hund's third rule). The second larger value also takes into account orbital polarisation (OP, Hund's second rule).
These XMCD experiments on paramagnetic dilute alloys of Co/Au at ID8 are the first direct measurements of the 3d magnetic moment which show that in cubic symmetry an appreciable amount of orbital magnetism may survive. The text book arguments about the quenching of orbital moments are derived on the basis of weak SOC, distinct separation of t2g and eg states as well as no intermixing. A strong hybridisation of the 3d impurity levels with the 5d host band structure and the delicate balance of the spin-up and spin-down filling of the 3d impurity bands can indeed explain this experimental finding. Nowadays, Co atoms or clusters on Cu(001) surfaces may be used to study the Kondo-effect on surfaces e.g. by means of scanning-tunnelling microscopy (STM). For future work of this kind it would be interesting to also consider the surviving orbital magnetism in these many-body effects.
References
[1] P. Gambardella et al., ESRF Highlights p. 85 (2003).
[2] G. Rado and H. Suhl (Eds.), "Magnetism", vol. 5, Academic Press New York/London (1973).
[3] B. T. Thole et al., Phys. Rev. Lett. 68, 1943 (1992); P. Carra et al., Phys. Rev. Lett. 70, 694 (1993).
Principal Publications and Authors
W.D. Brewer (a), A. Scherz (a), C. Sorg (a), H.Wende (a), K. Baberschke (a), P. Bencok (b), S. Frota-Pessôa (c), Phys. Rev. Lett. 93, 077205 (2004).
(a) Freie Universität Berlin (Germany)
(b) ESRF
(c) Universidade de São Paulo (Brazil)



