- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2004
- High Resolution and Resonance Scattering
- Diffusion in a Sub-monolayer Iron Film
Diffusion in a Sub-monolayer Iron Film
Atomistic details of diffusion processes can be monitored by scattering methods [1]. Destructive interference of the scattered radiation occurs when either the emitting probe atoms change their sites or the vicinity of the atoms changes temporally due to diffusion. From the way the interference is destructed, the atomistic details of the diffusion mechanism can be deduced. This idea has been successfully applied to study the motion of atoms and defects in the volume, i.e. in bulk material. The spectrum of methods used ranges from neutron scattering and Mössbauer spectroscopy to nuclear magnetic resonance and interference of synchrotron radiation. For selected cases the atomistic jump process was revealed, and today bulk diffusion can be regarded as principally well understood.
Recently the question of how atoms diffuse in lower-dimensional systems has attracted more attention. The consequences of surface diffusion are easily seen in images taken by a scanning tunnelling microscope (STM), but its mechanism can hardly be determined because of the limited time resolution of the STM which is of macroscopic dimensions, i.e. a few hundredths of seconds. Here synchrotron radiation comes into its own: Using short synchrotron radiation pulses we get access to the nanosecond regime and by applying nuclear resonance scattering we are able to study the slow dynamics, which in our case is diffusion.
Nuclear resonance techniques are element and even isotope sensitive, which means we get selective access to a single layer on the surface. Now we can employ some of the methods successfully developed for bulk material. Although technically this is more laborious than bulk studies because of lower count rates, there is an essential advantage offered by surfaces: motion of surface atoms is always motion in the vicinity of a vacancy defect the vacuum. For an atom embedded in the surface layer the broken symmetry at the surface induces an electric field gradient at the nuclear site with the main axis perpendicular to the surface. The orientation strongly depends on the nearest-neighbour co-ordination of the atom.
Exploiting this extreme case for the first time, we have studied surface diffusion by pursuing the fluctuation of the electric field gradient (beamline ID18). Figure 10 shows how a perturbation by an additional defect, such an embedded vacancy or an ad-atom, moving on the layer will result in a reorientation of the main axis of the electric field gradient. If the reorientation is sufficiently fast, the atom will feel an effective decrease of the electric field gradient (motional narrowing).
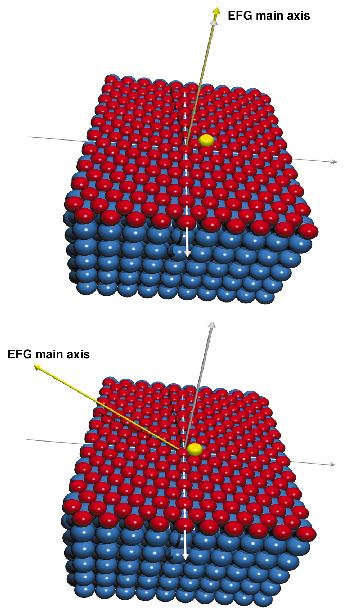 |
Fig. 10: Top: Model of a moving ad-atom on the surface. Perturbation of the intrinsic main axis of the electric field gradient (EFG) on an iron atom embedded in the uppermost layer. Bottom: The surrounding of the ad-atom changes with every jump. This causes a reorientation of the EFG main axis. |
In nuclear resonance scattering, the electrical field gradient is manifested by a beat pattern in the measured time spectrum. Figure 11 shows this pattern resulting from a sub-monolayer of iron on a tungsten substrate (single crystal W(110)). Arrows in Figure 11 indicate the clearly visible increase of the beat period after each temperature step between RT and 670 K. A RT spectrum was measured after each temperature step to check the structural stability of the sample and the reversibility of the effect. The analysis of the beat frequencies in the time spectrum favours the ad-atom diffusion compared to the vacancy exchange diffusion within the layer.
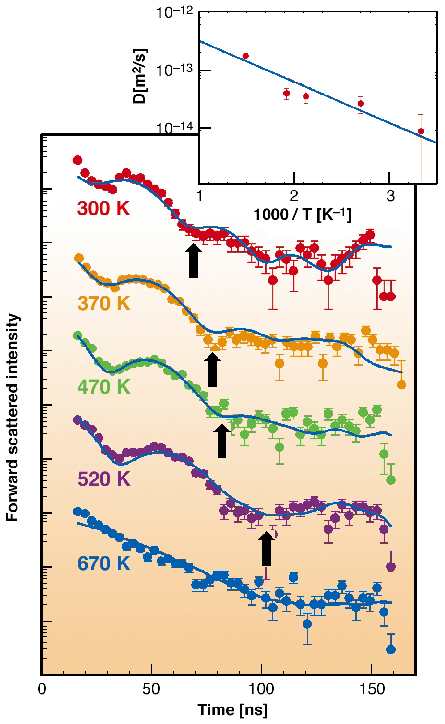 |
|
Fig. 11: Nuclear resonance scattering of synchrotron radiation: Time spectra for iron sub-monolayer (0.6 ML) on W(110) measured between RT and 670 K. The beat period indicated by black arrows increases clearly. The solid line is the fit achieved with an ad-atom model. The spectra are shifted relatively to each other in the vertical direction. The inset shows the calculated diffusion coefficient. |
To connect the increase of the beat period with the fluctuation frequency and finally with the jump frequency of atoms, the theory of Dattagupta and Schroeder [2] developed for bulk materials was modified for surfaces. In this way an Arrhenius diagram of the diffusion coefficient, assuming a nearest-neighbour jump diffusion mechanism of the ad-atoms, can be calculated. The Arrhenius plot with the activation energy 0.14(2) eV is shown in the inset of Figure 11.
Our study demonstrates the sub-monolayer sensitivity of the nuclear resonance scattering method and its ability to resolve fast (MHz) diffusion processes on surfaces with atomic resolution.
References
[1] G. Vogl and B. Sepiol, "The Elementary Diffusion Step in Metals Studied by the Interference of Gamma-rays, X-rays and Neutrons" in Diffusion in Condensed Matter, P. Heitjans and J. Kärger, (Eds), Springer (2005).
[2] S. Dattagupta and K. Schroeder, Phys. Rev. B 35, 1525 (1987).
Authors
M. Sladecek (a), B. Sepiol (a), J. Korecki (b,c), T. Slezak (b,c), D. Kmiec (a), R. Rüffer (d), G.Vogl (a).
(a) University of Vienna (Austria)
(b) AGH University of Science and Technology, Krakow (Poland)
(c) Institute of Catalysis and Surface Chemistry, Polish Academy of Science (Poland)
(d) ESRF



