- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- The X-ray Source
- Measurement of the Vacuum Chamber Coupling Impedance
Measurement of the Vacuum Chamber Coupling Impedance
The beam intensity in the storage ring is limited by several effects, depending on the filling pattern: thermal limitations, beam instabilities The beam instabilities are driven by the interaction of the electromagnetic field induced by the beam and its environment, typically the surrounding conductive vacuum chamber or RF cavities. This interaction is characterised by the so-called "coupling impedance", relating the perturbations seen by the beam, due to the presence of the vacuum chamber, to the beam intensity. For better performance, this impedance should be kept as low as possible. However, the finite conductivity of the chamber and any variation of the chamber cross-section will contribute to the impedance. The coupling impedance can be defined for any portion of the chamber, and all impedances add up to give the total ring impedance. Among the main contributions to this impedance, we can find:
- All narrow gap chambers, like low gap ID chambers, in-vacuum undulators, NEG coated chambers.
- RF accelerating cavities, bellows, flanges, tapers and transitions contributing to resonator-like objects in the impedance.
As discussed earlier, the stability of the single bunch mode of operation has been significantly reduced in the last two years since the installation of the 8mm aperture vacuum chambers got under way. In the long term about 20 of these chambers will be installed and the stability of the beam in the multibunch filling pattern could also be affected through the so-called resistive wall effect. It is therefore essential to follow the evolution of the storage ring impedance and to validate the technological choices of the ID chambers. Theoretical values of impedance can be computed at the design phase, but they require extensive numerical simulations and do not take into account the unavoidable imperfections. Recently, we started using a new method to measure the impedance of selected portions of the vacuum chamber [1].
The coupling impedance can be expressed by 3 complex functions of the frequency: the longitudinal impedance, related with bunch lengthening and longitudinal instabilities, and the horizontal and vertical impedances, related to tune shifts and transverse instabilities. The method we use applies to the vertical impedance (though it can also be used for horizontal impedance).
This method consists in displacing the beam vertically, using a static orbit deviation, to the place where we want to measure the impedance. The effect of the impedance is to induce an angular kick proportional to the displacement, the bunch intensity and the imaginary part of the effective impedance (impedance integrated over the bunch spectrum). This small kick is measured by subtracting the orbit deviations measured by displacing a low intensity beam (where the effect of impedance is negligible) and a high intensity beam. We use two different set-ups:
- Local measurements where we apply a local orbit bump and measure the impedance of a single straight section, including the adjacent dipoles.
- Global measurements where we apply a series of orbit oscillations probing the impedance all around the machine, and a processing extracting an impedance value for each straight section.
The final result is the imaginary part of the effective impedance. Though this number does not provide any information as to the behaviour of the impedance versus frequency, it is a relevant figure of merit for estimating the consequences on the beam.
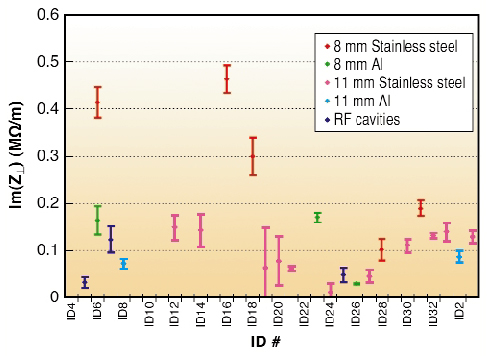
Figure 180 summarises the values measured since May 2003 using the global measurement set-up. It shows the reproducibility of the method and the properties of various types of straight sections.
 |
|
Fig. 180: Vertical effective impedance measured on several straight sections of the storage ring. |
The largest values are reached by some 8 mm internal aperture stainless steel chambers, with a large dispersion between the five similar chambers. Local measurements performed on a few straight sections are in good agreement with these values. Local measurements performed in the short straight section of the achromats confirm that the impedance is much lower in these areas.
In conclusion one could say that, unlike theoretical estimates, the direct measurement of impedances takes into account all fabrication errors and imperfections, resulting in a significant dispersion of measured values for identical vacuum chambers. The measured values are also larger than the theoretical estimates. This is especially true for stainless steel 8 mm aperture chambers. The aluminium 8 mm aperture chambers have a better behaviour and show consistently low values. Finally the measurements confirm the expected fact that the impedance is mainly localised in the small aperture insertion device straight sections, the short straight section of the achromats making a lower contribution.
Reference
[1] L. Emery, G. Decker, J. Galayda, PAC 2001, Chicago.



