- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- X-ray Absorption and Magnetic Scattering
- Giant Atomic Magnetic Anisotropy
Giant Atomic Magnetic Anisotropy
Magnetic materials play a key role in present-day technology and industry. In many instances their usefulness is determined by the magnetic anisotropy, i.e. by the extent to which the magnetisation retains or switches its orientation in response to thermal or magnetic stimuli. Owing to its importance, different sources of magnetic anisotropy have been investigated over the past 100 years. Studies on ferromagnetic bulk materials and thin films have highlighted the dependence of the magnetocrystalline anisotropy energy (MAE) on crystal symmetry and atomic composition [1]. While the exchange interaction among electron spins is purely isotropic, the orbital magnetisation, via the spin-orbit interaction, connects the spin magnetisation to the atomic structure of a magnetic material, hence giving rise to magnetic anisotropy [2]. Surface-supported nanoparticles offer additional degrees of freedom to tune the MAE by modifications of the particle size, shape, and coupling with the substrate. This makes nanosized systems attractive for basic investigations as well as for miniaturised data storage applications. To date, it is still unclear how anisotropic behaviour sets in and evolves in nanoscale particles. The key issues are the dependence of magnetic anisotropy on the details of the atomic coordination, its relation to the atomic magnetic moments, and the intrinsic upper limits to the MAE in a magnetic compound.
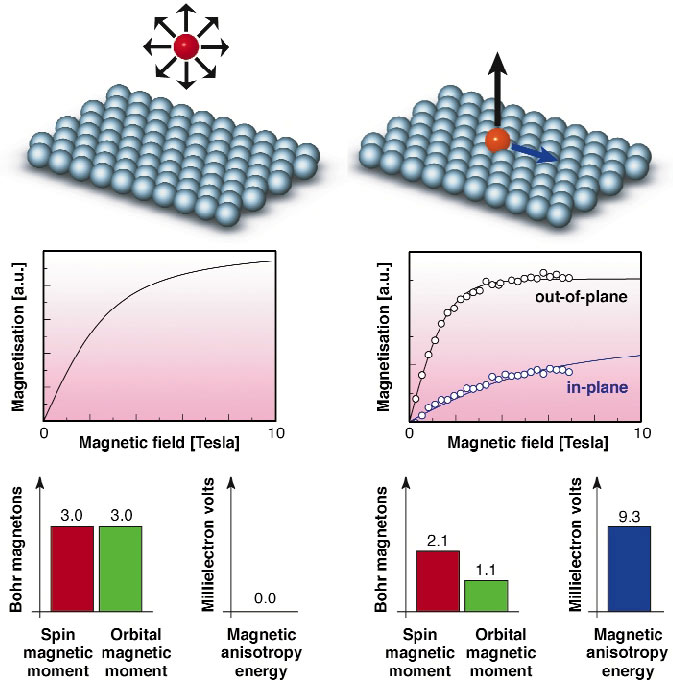
Gas phase atoms with unfilled electronic shells possess large spin (S) and orbital (L) magnetic moments according to Hund's rules and no magnetic anisotropy, owing to spherical symmetry (Figure 112). Experiments on beamline ID08 revealed the sudden appearance of magnetic anisotropy as a magnetic atom is deposited onto a nonmagnetic surface caused by symmetry reduction and interaction with the substrate electron states. X-ray magnetic circular dichroism (XMCD) measurements probed the magnetism of Co atoms deposited on a Pt(111) surface (Figure 113a). Application of the XMCD sum rules yields L = 1.1 ± 0.1 µB and S + 7 D = 1.8 ± 0.1 µB for single Co atoms, where D is the spin dipole moment. S is calculated in the LSDA scheme to be 2.1 µB. The unusually large orbital magnetisation compared to bulk Co (L = 0.15 µB) can be explained as a result of the reduced Co coordination [3], which allows the survival of Hund's-type correlations in the 3d orbitals.
 |
|
Fig. 112: Magnetisation of a gas phase Co atom (left) compared to that of a Co atom on a Pt surface (right). Co/Pt was chosen as a model system due to the large MAE of bulk CoPt alloys. Co atoms were deposited in situ in ultra-high-vacuum conditions on a Pt(111) surface at temperature T = 5.5 K in order to inhibit surface diffusion. |
The MAE of single Co atoms on Pt, obtained from quasi-static magnetisation cycles measured by XMCD at the L3 Co edge in the out-of-plane (easy) and in-plane (hard) directions, exceeds 9 meV/atom (Figure 112). This value is larger than that of any known magnetic compound, including bulk hcp Co (0.045 meV/atom) and SmCo5 (1.8 meV/Co atom). While the reduced symmetry of the Co adatoms as compared to the gas-phase constitutes the necessary condition to exhibit anisotropic behaviour, the magnitude of the MAE is attributed to the localisation of the 3d-electrons, which augments the spin-orbit energy due to increases in S and in the local density of states near the Fermi level, and to the strong 5d spin-orbit coupling of the neighbour Pt atoms.
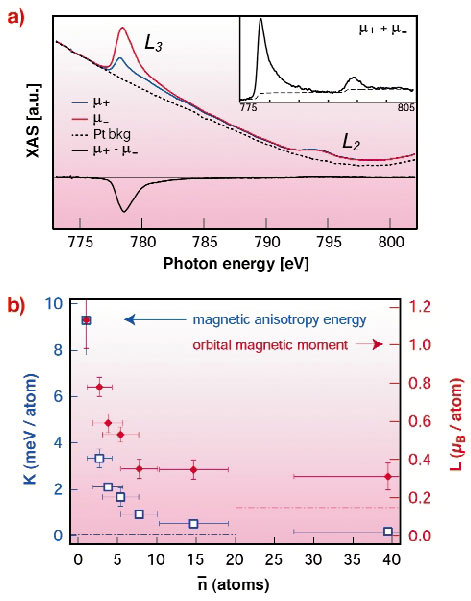
By assembling Co nanoparticles containing up to 40 atoms, the MAE was further shown to depend critically on the atomic coordination. The results plotted in Figure 113b demonstrate a clear correlation between the MAE and L, both decrease abruptly for single atom increments of the average cluster size. These results were matched by ab initio calculations and constitute a first step towards understanding how the magnetic anisotropy develops in finite-sized magnetic particles.
 |
|
Fig. 113: (a) XAS spectra recorded over the L2,3 edges of isolated Co atoms on Pt(111) with X-ray polarisation parallel (blue line) and antiparallel (red line) to a 7 T applied magnetic field at 5.5 K, and corresponding XMCD (black line). The inset shows the sum of the two XAS spectra after subtraction of the Pt background signal (solid line) with a two-step function for edge jump removal (broken line). (b) MAE, K, (squares) and orbital magnetic moment, L, (diamonds) as a function of the average size of two-dimensional Co clusters on Pt(111). The dashed lines represent the values of MAE and orbital moment for bulk hcp-Co (blue and red, respectively). |
References
[1] J. Kanamori, in Magnetism Vol. 1, edited by G.T. Rado and H. Suhl (Academic Press, New York 1963); U. Gradmann, in Handbook of Magnetic Materials Vol. 7, edited by K.H.J. Buschow (Elsevier, Amsterdam 1993).
[2] G. van der Laan, J. Phys.: Condens. Matter 30, 3239 (1997).
[3] P. Gambardella et al., Nature 416, 301 (2002).
Principal Publication and Authors
P. Gambardella (a,b), S. Rusponi (a,b), M. Veronese (c), S.S. Dhesi (d), C. Grazioli (c), A. Dallmeyer (e), I. Cabria (e), R. Zeller (e), P.H. Dederichs (e), K. Kern (a,b), C. Carbone (c,e) and H. Brune (a), Science 300, 1130 (2003).
(a) EPF Lausanne (Switzerland)
(b) MPI Stuttgart (Germany)
(c) CNR-ISM, Trieste (Italy)
(d) ESRF
(e) FZ Jülich (Germany)



