Thermal Fluctuations and Elasticity of Lipid Membranes

Lipid membranes are important model systems for biological membranes. They are intensively studied with regard to their structure, self assembly properties, phase behaviour, transport and elasticity properties, as well as their interaction with other macromolecules. From a statistical mechanics point of view they represent an interesting class of fluctuating quasi two-dimensional objects. Apart from k_BT, the thermal fluctuations are governed only by an intrinsic bending rigidity K. The effect of the thermal fluctuations on the positional correlations and the scattering intensity distribution has been worked out in the framework of linear elasticity theory (Caillé model) for stacks with periodic boundary conditions, as a function of K and the compressional modulus B (given by the second derivative of the interaction potential between two membranes at their equilibrium distance d). Recently, the model has been extended to include the boundary condition of a flat substrate on which a stack of lipids can be deposited [1].

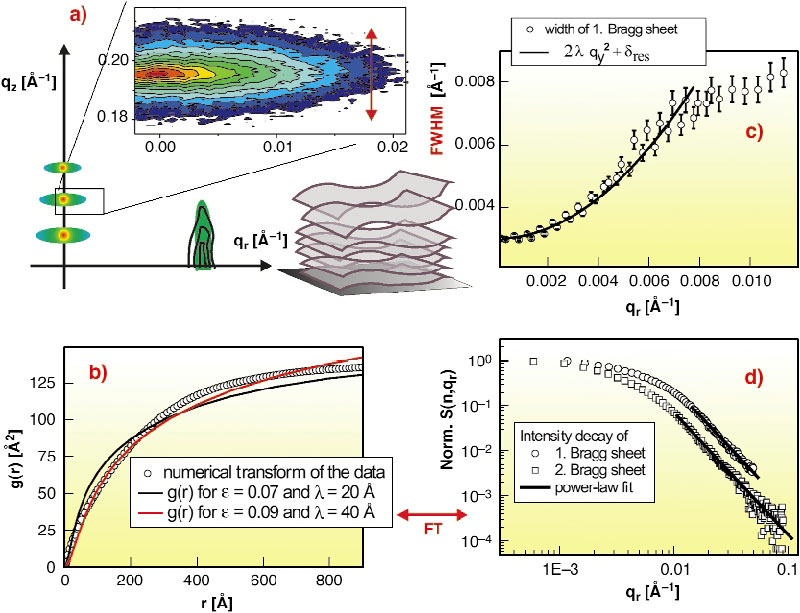
The present experiment on thermal fluctuations has been carried out on samples with several hundreds of highly-oriented lipid membranes deposited on silicon surfaces and studied at full hydration under excess water, both in the gel and the fluid L-phase. The main aim was to map the diffuse scattering over a wide range of momentum transfer, see Figure 88a, both in radial q_r (parallel to the plane of the membrane) and q_z. Diffuse X-ray reflectivity measurements using 20 keV synchrotron beams have been carried out at the undulator beamline ID01, using both a fast scintillation counter and a multwire area detector. Data was collected mainly on the uncharged lipids dimyristoyl-sn-Glycero-Phosphocholine (DMPC) and oleoyl-Palmitoyl-sn-Glycero-Phos-phocholine (POPC), and also on charged phospholipids [2]. For data acquisition, angles of incidence were chosen that do not excite specular Bragg peaks. The typical intensity distribution on the CCD detector then consists of only a weak specular beam and two to four strong equidistant diffuse Bragg sheets. From the q_z value, the mean distance d can be obtained, i.e. for fully-hydrated DMPC membranes d ~ 63 Å, corresponding to a water layer of about 25 Å in between adjacent membranes. Importantly, the width (HWHM) of the diffuse Bragg sheets along q_z increases quadratically with q_r, before it saturates to at high q_r, see Figure 88c for a typical data set. The quadratic increase (solid line) is in line with the theoretical prediction and its steepness is given by the fundamental smectic length = (K /Bd)^0.5. From the analysis of the q_z-integrated intensity with q_r the height-height correlation function was calculated using a back transformation method. The resulting curve for DMPC in the fluid phase is shown in Figure 88c along with theoretic curves (solid lines) [1]. The parameters k and B can be chosen to fit the curves at small, intermediate or large r, but should be regarded as effective parameters, which can vary significantly since the model cannot account for all data simultaneously. Note that this conclusion is currently a matter of debate [3].

Fig. 88: (a) Typical diffuse scattering distribution of multilamellar lipid bilayers (DMPC, fluid phase). (b) Characteristic height-height self-correlation function of an averaged membrane in the stack as derived from the data, together with theoretic function acc. to [1]. (c) Increase in the width (vertical qz-width) of the first Bragg sheet. (d) Decay of the (qz-) integrated intensity of the the first two Bragg sheets n = 1 and n = 2.

Already on the level of the raw data, deviations from the predicted behavior is observed: (i) the power law exponent of the intensity decay shown in Figure 88d, and (ii) the saturation of the Bragg sheet width shown in Figure 88b. Both are observed at parallel wave vector components which where not accessible before (in unoriented bilayers or and at less brilliant sources). Therefore we must conclude that fluctuations on the corresponding length scales are not well described by the Caillé model. A number of reasons could limit the applicability of the model: (i) non-bending collective motions, (ii) non-linear elasticity terms, (iii) a length scale dependence of K , (iv) breakdown of the mean field approach. Alternative more rigorous theories (renormalisation group theories, self-consistent theories) and computer simulations on reasonably large stacks of membranes and lateral system size may help to gain more understanding. On the experimental side, the studies of diffuse scattering are currently extended to cover also charged lipids and lipid/peptides mixtures.

References
[1] D. Constantin, U. Mennicke, C. Li, and T. Salditt, EPJE 12, 283 (2003).
[2] G. Brotons, T. Salditt, M. Dubois, Th. Zemb, Langmuir 19, 8235-8244 (2003).
[3] G. Pabst, comment on PRL 90, 178101 (2003), submitted; T. Salditt, M. Vogel, W. Fenzl, Reply to comment by Pabst, submitted.

Principal Publication and Authors
T. Salditt (a), M. Vogel (b), W. Fenzl (b), Physical Review Letters 90, 178101 (2003).
(a) Universität Göttingen (Germany)
(b) Max-Planck-Institut für Kolloid- und Grenzflächenforschung Golm (Germany)