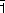- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- Materials Science
- Temperature-induced Valence Transition in Intermediate Valence Sm2.75C60
Temperature-induced Valence Transition in Intermediate Valence Sm2.75C60
Metal intercalation compounds of C60 are narrow band systems whose understanding poses considerable challenges owing to the dominant role of electronic correlations [1]. Rare-earth fullerides further constitute an intriguing class of strongly correlated electron systems because, in addition to the electronically active anion (C60) sublattice, they accommodate a highly correlated cation (rare-earth) sublattice.
A prominent example of a rare-earth fulleride is Sm2.75C60 which adopts a complex orthorhombic structure (space group Pcab) characterised by long-range ordering of tetrahedral samarium vacancies and orientational ordering of C60 about local three-fold symmetry axes (Figure 38). When we probed the structural properties of Sm2.75C60 by high-resolution X-ray diffraction on beamline ID31, we found that it exhibits isotropic negative thermal expansion (NTE) in the temperature range 4.2 to 32 K. The NTE coefficient reaches values two orders of magnitude higher than those observed in metal oxides like ZrW2O8 [2]. We attribute the origin of the lattice collapse on heating to a quasi-continuous isosymmetric phase transformation driven by the temperature-induced valence transition of Sm from +2 to an intermediate valence of +(2+![]() ). This effect is reminiscent of the pressure-induced valence transitions in intermediate-valence Kondo insulators like SmS [3].
). This effect is reminiscent of the pressure-induced valence transitions in intermediate-valence Kondo insulators like SmS [3].
 |
|
Fig. 38: Building block of the orthorhombic superstructure of Sm2.75C60, which can be obtained by doubling along all three lattice directions. Distorted octahedral and tetrahedral samarium cations are depicted as green and blue spheres, respectively. The tetrahedral samarium defect (~ 25% occupancy) is shown as red sphere. The five symmetry-inequivalent C60 units present in the unit cell (C60(1) at (000), C60(21) at (01/41/4), C60(22) at (1/401/4), C60(23) at (1/41/40) and C60(3) at (1/21/21/2)) are optimally rotated anticlockwise by 37.5° about local three-fold symmetry axes ([111], [1 |
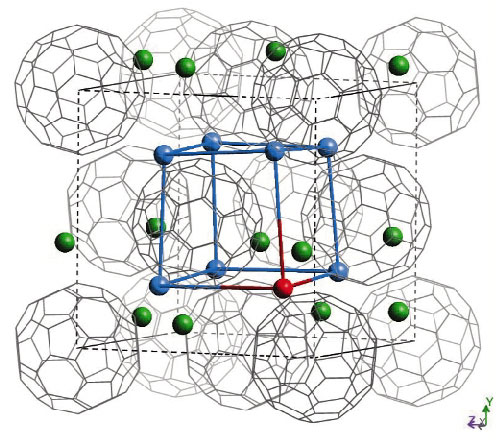
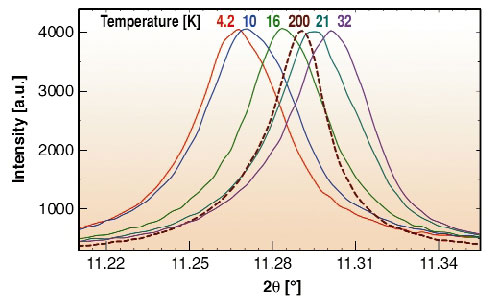
The lattice response is evident when we follow the behaviour of the (444) Bragg peak as a function of temperature (Figure 39). At low temperatures, its position continuously shifts to higher angles on heating, implying anomalous structural behaviour whereby the material contracts as the temperature increases. The trend is reversed above 32 K and normal behaviour is restored with the lattice expanding on heating to 295 K. However, no changes in peak intensities are apparent in the whole temperature range, implying the absence of a phase transition to a structure with different crystal symmetry. Structural analysis at all temperatures resulted in the evolution of the unit cell volume shown in Figure 40. Initially the lattice contracts slowly on heating above 4.2 K.
 |
|
Fig. 39: Selected region of the diffraction profile of Sm2.75C60 showing the temperature evolution of the (444) Bragg reflection (
|
Then the rate of contraction increases to ![]() V ~ -1000 ppm K-1 resulting in a volume decrease of 0.84% between 4.2 and 32 K. The sign of the thermal expansivity then changes and the lattice expands on heating to 295 K at approximately +20 ppm K-1, comparable to that in other metal fullerides. Despite this, the Sm2.75C60 lattice dimensions at room temperature are smaller than those at 4.2 K.
V ~ -1000 ppm K-1 resulting in a volume decrease of 0.84% between 4.2 and 32 K. The sign of the thermal expansivity then changes and the lattice expands on heating to 295 K at approximately +20 ppm K-1, comparable to that in other metal fullerides. Despite this, the Sm2.75C60 lattice dimensions at room temperature are smaller than those at 4.2 K.
 |
|
Fig. 40: Temperature evolution of the orthorhombic unit cell volume of Sm2.75C60. The inset shows the temperature dependence of the coefficient of thermal expansion, |
The explanation of the remarkable lattice response of Sm2.75C60 comes from the fragility of the valence states of Sm and its tendency to exhibit intermediate valence. Firstly we note that the unit cell size of metal fullerides is sensitively controlled by the size of the ions residing in the small tetrahedral interstices. In Sm2.75C60, the tetrahedral hole has a radius of 1.12 Å, straddling the values of the ionic radii of Sm2+ (1.14 Å) and Sm3+ (0.96 Å). A valence transition of Sm from +2 towards an intermediate value of +(2+![]() ) with smaller ionic size, induced on heating, has a profound effect on the lattice size and is consistent with the observed dramatic volume decrease. Complementary magnetic susceptibility measurements provide an estimate of the average Sm valence at high temperatures as ~ +2.3.
) with smaller ionic size, induced on heating, has a profound effect on the lattice size and is consistent with the observed dramatic volume decrease. Complementary magnetic susceptibility measurements provide an estimate of the average Sm valence at high temperatures as ~ +2.3.
The results presented here open the way for the synthesis and study of new families of molecular-based highly-correlated Kondo and heavy fermion systems with strong coupling between the charge, lattice and spin degrees of freedom. What is unprecedented in the present fulleride analogue is that intermediate valence behaviour is encountered in a system for which strong correlations dominate the electronic properties of both the rare-earth cation and C60 anion sublattices. Such synergy has not been encountered before and the rare-earth fullerides should have properties intrinsically unattainable in comparable rare-earth chalcogenides with closed shell anions.
References
[1] O. Gunnarsson, Rev. Mod. Phys. 69, 575 (1997).
[2] T.A. Mary et al., Science 272, 90 (1996).
[3] A. Jayaraman et al., Phys. Rev. Lett. 25, 1430 (1970).
Principal Publication and Authors
J. Arvanitidis (a), K. Papagelis (a), S. Margadonna (b), K. Prassides (a), A.N. Fitch (c), Nature 425, 599-603 (2003).
(a) University of Sussex (UK)
(b) University of Cambridge (UK)
(c) ESRF