- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- High Resolution and Resonance Scattering
- Thermal-motion-induced Scattering from Zinc Oxide
Thermal-motion-induced Scattering from Zinc Oxide
One of the greatest virtues of the X-ray diffraction technique is that measurements can usually be related directly to the density of electrons in a material a property of fundamental importance to many areas of science. However, hidden in the finest details of the scattering, and its dependence on X-ray energy and polarisation, lies an array of increasingly complex and subtle physical phenomena. The most well known of these include magnetic scattering, and the signatures of orbital ordering in some metal oxide crystals [1]. Usually, these observations are made possible by measuring at positions where the 'normal' strong scattering is completely eliminated by the symmetry of the material under investigation.
Taking this approach to the next level, one can find reflections for certain crystal structures where the simplest (and strongest) scattering mechanism is subtler still, and must be described mathematically by a tensor of third rank. Two physical processes have been put forward for explaining the presence of such a signal: a mixed dipole-quadrupole resonance [2] and thermal-motion-induced scattering [3] (Figure 18). Both of these effects are of considerable importance in solid state physics, and, perhaps, co-exist in germanium [4]. Strangely, though, the resonance spectrum of germanium lacks significant structure or temperature dependence.
 |
|
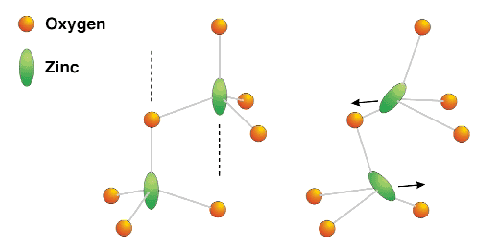
Fig. 18: Thermal-motion-induced scattering in ZnO. In the absence of thermal motion, the (anisotropic) scattering from zinc atoms related by glide-reflection symmetry cancels exactly for certain reflections (left). Dotted lines indicate three-fold rotation axes. Optical phonon modes cause the zinc atoms to move relative to the oxygens (right), inducing opposite tilts in the ellipses that characterise their resonance response. The symmetry between the scattering from each zinc atom, and hence the cancellation of the scattered wave, is broken by the different orientations of the ellipses with respect to the X-ray polarisation.
|
In contrast, we have observed, on BM28, very different behaviour of forbidden reflections in the wide-gap semiconductor, zinc oxide. The resonance spectrum of forbidden scattering highly structured, and it exhibits a very strong variation with temperature (Figure 19). The results are found to be in remarkably good agreement with a phenomenological model, proposed in [3]. In this model the total scattering is derived from a combination of temperature-independent (dipole-quadrupole) amplitude, and a second amplitude that scales with the average atomic displacement due to optical phonons, and therefore increases with temperature. By applying this analysis, we were able to extract not only the relative magnitude of the two processes, but also their relative phase. We find that the amplitudes mostly interfere destructively, and this explains the tendency of the scattering strength to drop initially as temperature is increased, before rising sharply.
 |
|
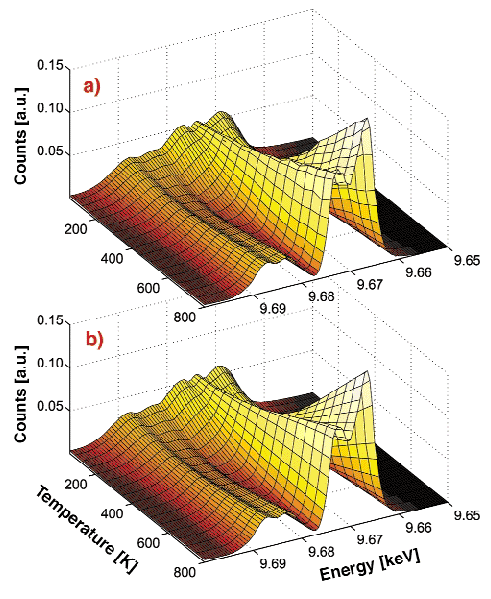
Fig. 19: a) The variation in the resonance spectrum of the ZnO 115 'forbidden' reflection with temperature, showing features that strengthen sharply with temperature, features that weaken, and others that vary very little. b) The results of a fit to a phenomenological based on the interference of two amplitudes thermal-motion-induced scattering and mixed dipole-quadrupole scattering. Differences between the measured signals and calculations are so small as to be barely visible. |
Both physical processes are of immense interest. Mixed dipole-quadrupole resonances vanish in the absence of hybridisation, and therefore provide a direct signature of mixing of electronic valence states. The thermal-motion-induced scattering amplitude is perhaps even more unique as it depends on the change in resonance response with atomic position a spectroscopy that has not previously been available. Detailed theoretical calculations are being developed to compare with these results, and further experiments are planned in order to study related materials, and similar effects that may arise from point-defects in crystals.
References
[1] S. Ishihara and S. Maekawa, Repts. Prog. Phys. 65, 561 (2002).
[2] D.H. Templeton and L.K. Templeton, Phys. Rev. B 49, 14850 (1994).
[3] V.E. Dmitrienko, E.N. Ovchinnikova, and K. Ishida, JETP Lett., 69, 938 (1999).
[4] J. Kokubun et al. Phys. Rev. B 64, 073203 (2001); A. Kirfel et al. Phys. Rev. B 66, 165202 (2002).
Principal publication and Authors
S.P. Collins (a), D Laundy (b), V.E. Dmitrienko (c), D. Mannix (d) and P. Thompson (d), Phys. Rev B 68, 064110 (2003).
(a) Diamond Light Source Ltd (UK)
(b) Daresbury Laboratory (UK)
(c) Institute of Crystallography, Moscow (Russia)
(d) XMaS UK CRG, ESRF



