- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- High Resolution and Resonance Scattering
- Inelastic X-ray Scattering in Cs under Pressure
Inelastic X-ray Scattering in Cs under Pressure
At ambient conditions, the alkali metals are considered as prototype examples of nearly-free-electron metals, the so-called "simple metals". All of them adopt the high-symmetry body-centred cubic (bcc) crystal structure. Pressure-induced structural phase transitions in the alkali metals have been studied in much detail since Bridgman's pioneering works on Cs in the 1930's. Under pressure, all alkali metals undergo a transition to the face-centred cubic (fcc) structure and subsequently to a variety of lower-symmetry structures. In recent years, very complicated crystal structures of several high-pressure phases of the heavier alkali elements have been observed a brief overview is given in [1].
Theoretical treatments have been quite successful in reproducing the observed structural sequences as a function of pressure. Most of these studies considered the energetics of the static lattice. Structural transitions may, however, also be driven by dynamical instabilities due to phonon softening near or at the Brillouin-zone boundary. In the case of Cs, this issue was addressed in recent theoretical investigations [2]. Their central result is the prediction of a pronounced phonon softening near the upper limit of the fcc-Cs stability range (~ 4 GPa) that could lead to a dynamical instability of the fcc phase with increasing pressure. Hardly any experimental data have been available to test these important and unexpected predictions.
Therefore we performed an inelastic X-ray scattering (IXS) study of the longitudinal acoustic (LA), Q = (1 0 0) phonons in the bcc and fcc phases of Cs at pressures up to 4 GPa (upper stability limit of fcc Cs), at beamline ID28. The monochromatic beam with a photon energy of 17.8 keV was focused onto a 250-µm Cs sample in a diamond anvil cell (DAC). The scattered photons were analysed by a high-resolution Si analyser giving an overall spectral resolution of 3.0 meV. Cs crystals were grown in the DAC by heating the Cs sample close to its melting line and then cooling it slowly to ambient temperature. The in situ crystal growth was monitored by X-ray diffraction at the beamline ID09.
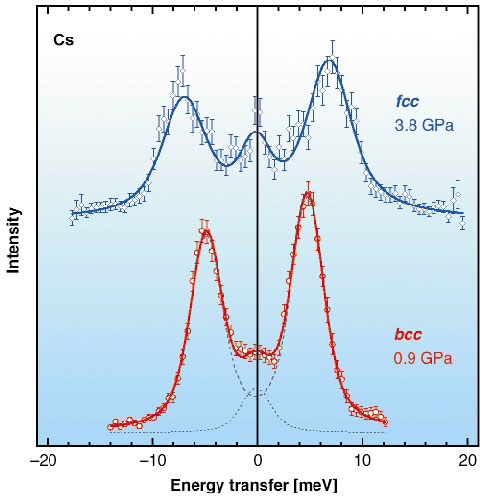
The IXS spectra of bcc and fcc Cs (Figure 4) exhibit well-defined Stokes- and anti-Stokes peaks of the LA zone-boundary phonons. It should be noted that the ambient-pressure phonon energy of ~ 4 meV (~ 30 cm1) is rather small, which made the experiment quite challenging.
 |
|
Fig. 4: Inelastic X-ray scattering spectra of Cs at Q = (1 0 0) in its bcc and fcc phases (T = 300 K). The open symbols represent the experimental data. The solid line corresponds to the best fit to a model function composed of Lorentzians for the phonon contribution (dashed lines) and the elastic contribution (dotted line), convoluted with the experimental resolution function. |
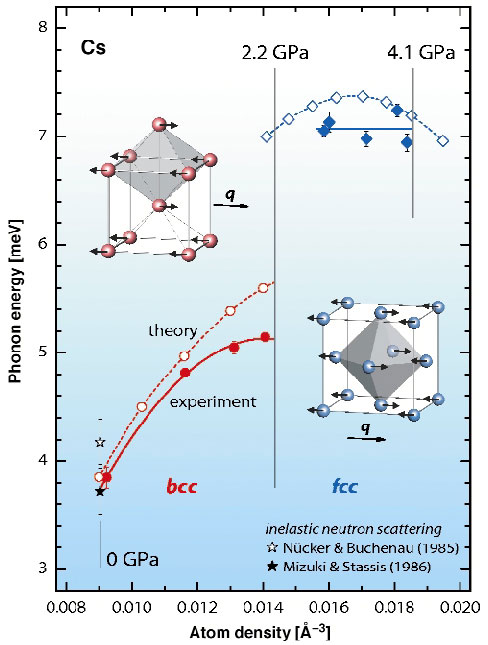
The pressure dependences of the phonon energies are depicted in Figure 5. In the bcc phase, the phonon frequency initially increases with pressure as expected, but with a slope approaching zero near the bccfcc transition. In the fcc phase the LA-(1 0 0) phonon frequency is pressure independent within the experimental uncertainty.
Our experiments were complemented by first-principles calculations. They also indicate an anomaly near the bccfcc transition (Figure 5), although not quite as pronounced as in the experiment. The general picture that emerges from the experimental and theoretical results is that of (i) a gradual decrease of the pressure dependence of the bcc LA-(1 0 0) phonon frequency when the bccfcc transition is approached and (ii) an anomalously small pressure dependence in the fcc phase, with a small softening near the upper fcc stability limit in the calculation. This picture is consistent with experimental results on the spatially averaged sound velocities in polycrystalline Cs at high pressures by Voronov et al. [3].
 |
|
Fig. 5: Experimental and calculated phonon energies of Cs in the bcc and fcc phases. Solid symbols and lines refer to the experimental data, open symbols and dashed lines to the theoretical data. |
The inelastic X-ray scattering experiments and corresponding calculations outlined here provide clear evidence of anomalies in the lattice dynamics of Cs near the bccfcc phase transition and in the fcc-phase. These results substantiate and refine the unexpected predictions of recent theoretical work, and they appear to be relevant also for other heavy alkali metals.
References
[1] K. Syassen in Proceedings of the International School of Physics "Enrico Fermi" Course CXLVII, Eds. R. J. Hemley et al., pp 251273 (2002).
[2] N. E. Christensen et al., J. Phys.: Condens. Matter 12, 3293 (2000) & Phys. Rev. B 61, R3764 (2000); J. Xie et al., Phys. Rev. B 62, 3624 (2000); Y. Kong and O. Jepsen, J. Phys.: Condens. Matter, 12, 8973 (2000).
[3] F. F. Voronov, O. V. Stal'gorova, and E. L. Gromnitskaya, J. Exp. Theor. Phys., 95, 77 (2002).
Principal Publication and Authors
I. Loa (a), K. Kunc (a), K. Syassen (a), M. Krisch (b), A. Mermet (b), and M. Hanfland (b), High Pressure Res. 23, 1 (2003).
(a) MPI für Festkörperforschung, Stuttgart (Germany)
(b) ESRF



