- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2002
- X-ray Absorption and Magnetic Scattering
- A New Computational Scheme for X-ray Absorption Spectroscopy in Strongly-correlated Systems
A New Computational Scheme for X-ray Absorption Spectroscopy in Strongly-correlated Systems
Multiple scattering (MS) theory provides an accurate and flexible scheme for the calculation of unoccupied electronic states, which are probed by various synchrotron experiments such as X-ray absorption spectroscopy and resonant X-ray scattering.
The standard theory relies on the single-particle picture: that is, it neglects electron correlation effects. This is a great shortcoming, since core-level X-ray spectra are often strongly modified by electron correlation, in particular by the Coulomb and exchange interaction of the valence electrons with the core hole. In transition metal and rare earth systems, this interaction can give rise to pronounced atomic multiplet and satellite structures in the spectra, which can only be accounted for in a many-electron calculation.
A generalisation of MS theory to many-electron wave functions was developed by Natoli et al. [1]and is known as "multichannel" MS theory. The idea is to develop the photo-absorption final state over a basis of corresponding photo-ionisation final states, i.e. over the eigenstates of the N1 electron system with one core-hole but without the photo-electron. In a given photo-absorption process, the final state energy and all other conserved quantum numbers can be distributed in different ways between the N1 electron system and the photo-electron; each of these different ways is called a channel. Since the photo-electron is correlated with the N1 other electrons through exchange and Coulomb interaction the channels are coupled.
Within the multichannel MS framework, we have developed a relatively simple method that allows one to take into account atomic multiplet effects due to the interaction between the photo-electron and electrons/holes in sufficiently-localised orbitals. Sufficiently localised means that the wave function is negligibly small beyond the atomic radius. This applies exactly to inner-core shells and well to the 4f-shell in rare earths. Whether the same approach may also be used for the interaction with 3d-electrons in transition metals is not clear at this point.
Short Outline of the Formalism
The systems' ground state is described by an N-electron wave function, where all N electrons are in core- or sufficiently-localised valence-shells. Electrons in wide valence bands are not explicitly taken into account; their effect on the photo-electron wave function is treated in a mean-field approximation as in standard MS theory. In the final state of the photo-absorption process N1 electrons remain in localised orbitals and one is promoted to a delocalised (conduction band) orbital.
Atomic multiplet calculations are performed to determine the ground state with energy Eg and the eigenstates of the N1 electron system, | >, with energies E
>, with energies E . For given total final state energy E = Eg +
. For given total final state energy E = Eg + 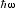 , N-electron basis states |
, N-electron basis states | ,ilm
,ilm > are defined as anti-symmetrised product states between |
> are defined as anti-symmetrised product states between | > and |
> and |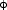 i,,ilm
i,,ilm >, where
>, where 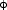 stands for a small set of orthogonal orbitals for each orbital quantum number l. With these |
stands for a small set of orthogonal orbitals for each orbital quantum number l. With these | ,ilm
,ilm >, the so-called eigen-channel method [2] is employed for the calculation of the atomic T-matrices and the optical transition matrix elements. Once the latter quantities are known, the MS formalism extends in a straightforward way to the multichannel case [1].
>, the so-called eigen-channel method [2] is employed for the calculation of the atomic T-matrices and the optical transition matrix elements. Once the latter quantities are known, the MS formalism extends in a straightforward way to the multichannel case [1].
Within the restrictions about the localisation of orbitals stated above, we have shown how the eigen-channel method, so far only used in atomic and nuclear physics, can be applied to X-ray absorption in condensed systems.
Due to the localised character of the core-hole, the most important correlation effects are often local to the absorbing atom. This means that the multichannel nature of the T-matrix needs to be taken into account for this one atom only.
We have shown that in this important case, the MS equations can be be solved very efficiently using a partitioning technique. The numerical difficulty of the whole multichannel problem is then reduced to that of a standard MS problem (for the system without absorber) plus a multichannel but purely atomic problem.
Implementation of the formalism in computer code is in progress. First applications include X-ray absorption spectra of light transition metal compounds at the L2,3 edges, and magnetic circular dichroism of rare-earth compounds at the rare-earth X2,3 (X = L,M,N) and ligand K edges. In these cases, standard MS theory fails to reproduce the observed spectra line shapes. The failure is believed to be due to atomic multiplet-like interactions between the photo-electron and the core-hole or the 4f electrons, which can be taken into account completely by our new method.
References
[1] C.R. Natoli, M. Benfatto, C. Brouder, M.F.R. López, and D.L. Foulis, Phys. Rev. B 42, 1944 (1990).
[2] M. Aymar, C.H. Greene, and E. Luc-Koenig, Rev. Mod. Phys. 68, 1015 (1996).
Principal publication and Authors
P. Krüger (a) and C.R. Natoli (b), to be published.
(a) ESRF
(b) INFN, frascati (Italy)



