- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2002
- Soft Condensed Matter
- Glass Microspheres Generate Perfect Aperiodic Order
Glass Microspheres Generate Perfect Aperiodic Order
Self-organisation of colloidal hard spheres into crystalline structures provides an important model of atomic crystal growth and attracts significant attention as a technique for inexpensive, large-scale fabrication of photonic materials [1]. A crystal is said to be perfect when the positions of the "atoms" (in the present case the micro-spheres) are correlated throughout the whole crystal despite their thermal motion. In reality, however, most crystals are not perfect [2]. Although local order may be apparent, various defects or strain fields can easily destroy order on a large scale. Moreover, the colloidal spheres are non-identical as there is slight variation in their sizes, which may also affect the long-range order. To date, confocal optical microscopy has provided essential information on the local order in colloidal crystals, while order on a large scale was rarely addressed. The latter can be determined by diffraction techniques from the width 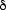 q of the reciprocal lattice reflections. Colloidal crystals are a particularly challenging subject for X-ray studies because the sub-micrometre "atoms" are more than three orders of magnitude larger than the wavelength
q of the reciprocal lattice reflections. Colloidal crystals are a particularly challenging subject for X-ray studies because the sub-micrometre "atoms" are more than three orders of magnitude larger than the wavelength 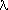 (in this work the silica spheres had a diameter of 224 nm and
(in this work the silica spheres had a diameter of 224 nm and 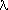 = 0.124 nm). For crystals possessing positional order over distances
= 0.124 nm). For crystals possessing positional order over distances 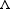 as large as 103 lattice periods, the width
as large as 103 lattice periods, the width 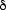 q of the diffraction peaks is smaller than one millionth part of the X-ray wavevector k0 = 2
q of the diffraction peaks is smaller than one millionth part of the X-ray wavevector k0 = 2 /
/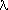 = 50 nm1. The results obtained at beamline BM26B "DUBBLE CRG" demonstrate that such a resolution is readily achievable in a small-angle X-ray diffraction experiment on a single colloidal crystal.
= 50 nm1. The results obtained at beamline BM26B "DUBBLE CRG" demonstrate that such a resolution is readily achievable in a small-angle X-ray diffraction experiment on a single colloidal crystal.
 |
|
Fig. 17: (a) Bragg reflections of light from colloidal crystals in a flat capillary (cross section 0.2 x 4 mm2); (b-d) two-dimensional structure factors (X-ray diffraction intensity divided by the single sphere form factor) obtained from the large crystal in the middle of the capillary in (a). In (b) the incident beam is normal to the hexagonal planes. The sample is tilted by 0.2° in (c) and by 0.3° in (d). |
The apparent width of the reflections ~3 x 103 nm1 on the detector (Figure 17) is limited by the instrumental resolution rather than by the crystal order in the transverse direction. Rocking the crystal by a tiny angle around one of the low-index orientations is found to lead to significant modification of the pattern, which does allow for accurate determination of the width 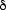 q of the reflections in the longitudinal direction (along the beam). In our small-angle diffraction geometry (maximum diffraction angle 2
q of the reflections in the longitudinal direction (along the beam). In our small-angle diffraction geometry (maximum diffraction angle 2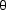 in Figure 17 is ~ 0.5°), the curvature of the relevant part of the Ewald sphere is extremely small. However, due to the smallness of
in Figure 17 is ~ 0.5°), the curvature of the relevant part of the Ewald sphere is extremely small. However, due to the smallness of 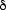 q, it is clearly visible in (c) and (d) yielding an asymmetric diffraction pattern. The brightest reflections are found along a circle where the Ewald sphere is intersected by a plane of reciprocal lattice nodes. Detailed analysis of the data shows that in fact
q, it is clearly visible in (c) and (d) yielding an asymmetric diffraction pattern. The brightest reflections are found along a circle where the Ewald sphere is intersected by a plane of reciprocal lattice nodes. Detailed analysis of the data shows that in fact 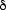 q < 5 x 105 nm1 suggesting long-range interplanar positional order throughout the sample thickness. Sample translations revealed only small modifications of the diffraction pattern within the same single crystal. This result indicates high (within 0.1°) orientational correlation over distances larger than a millimetre suggesting high rigidity of the hexagonal planes.
q < 5 x 105 nm1 suggesting long-range interplanar positional order throughout the sample thickness. Sample translations revealed only small modifications of the diffraction pattern within the same single crystal. This result indicates high (within 0.1°) orientational correlation over distances larger than a millimetre suggesting high rigidity of the hexagonal planes.
The crystal was found to possess a randomly-stacked hexagonal close-packed (rhcp) structure. Due to irregular stacking, some features of the reciprocal lattice of an rhcp crystal are smeared out into Bragg scattering rods while periodicities common to all layers lead to sharp Bragg spots, which are both clearly visible in the structure factor profile (Figure 18). The intensity modulation along the rods is also typical for rhcp crystals [2].
 |
|
Fig. 18: (a) Reciprocal lattice of rhcp crystals. The shadowed planes are to guide the eye. (b) Sets of Bragg spots and Bragg rods in the structure factor measured with X-rays propagating along the hexagonal crystal planes. |
In summary, various order parameters of single colloidal crystals are determined by small-angle X-ray diffraction with a resolution of 106k0. The glass microspheres are found to organise themselves into flat hexagonal layers, which are randomly stacked. Despite the lack of periodicity, perfect interplanar positional order is demonstrated.
References
[1] Y.A. Vlasov et al., Nature 414, 289 (2001).
[2] A. Guinier, X-ray Diffraction in Crystals, Imperfect Crystals and Amorphous Bodies, Dover Publications (1994).
Principal Publication and Authors
A.V. Petukhov (a), D.G.A.L. Aarts (a), I.P. Dolbnya (b), E.H.A. de Hoog (a), K. Kassapidou (a), G.J. Vroege (a), W. Bras (b) and H.N.W. Lekkerkerker (a), Phys. Rev. Lett. 88, 208301 (2002); ibid 90, 028304 (2003).
(a) Van't Hoff Laboratory for Physical and Colloidal Chemistry, Utrecht (The Netherlands)
(b) DUBBLE CRG, ESRF



