- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2002
- Methods and Instrumentation
- Two-dimensional X-ray Waveguides
Two-dimensional X-ray Waveguides
We have carried out a proof of principle experiment demonstrating that resonant coupling of synchrotron beams into suitable nanostructures can be used for the generation of coherent X-ray point sources. To this end, a rectangular, two-dimensionally (2D) confining X-ray waveguide structure has been fabricated by electron-beam lithography. Shining a parallel undulator beam onto the structure, a discrete set of resonant modes can be excited in the dielectric cavity, depending on the two orthogonal coupling angles between beam and the waveguide interfaces. The resonant excitation of the modes is evidenced from the characteristic set of coupling angles as well as the observed far-field pattern. The device thus delivers a coherent X-ray beam of 68.7 nm x 33.0 nm cross-section (horiz. and vert. FWHM) at the exit of the cavity.
Planar X-ray waveguide structures have been demonstrated as new tools to produce coherent and divergent X-ray beams with cross-sections in the sub-micrometre range in one dimension [1-3]. However, for many nanomicroscopy and nanospectroscopy applications, a two-dimensionally-confined point beam instead of one-dimensional line beam is needed.
In recent experiments carried out at undulator beamline ID13 we have demonstrated for the first time that a two-dimensional beam compression using the resonant beam coupling principle can be achieved. Applying state-of-the-art electron-beam lithography techniques, we have fabricated laterally and vertically patterned nanostructures, where the beam is channelled in two-dimensions. Figure 120 shows a schematic of such an 'X-ray fibre' consisting of a spin-coated, rectangular patterned PMMA core coated with evaporated Cr metal on silicon substrate. In the experiments, waveguides of cross sections down to 33 nm x 68 nm were measured.
 |
|
|
Just like in the optical analogue, the resonantly-enhanced electromagnetic field distribution of an X-ray waveguide can be described by a set of discrete and precisely-defined modes (at the respective angles ai and fi), which are determined by the geometry of the structure and the choice of materials. Accordingly, the guided modes are excited by shining a parallel beam onto the waveguide at grazing incidence at a set of angles  i,n and
i,n and  i,m. A coherent beam exists and the structure at the side has a cross-section corresponding to the thickness of the guiding layer and a divergence in the range of some mrad.
i,m. A coherent beam exists and the structure at the side has a cross-section corresponding to the thickness of the guiding layer and a divergence in the range of some mrad.
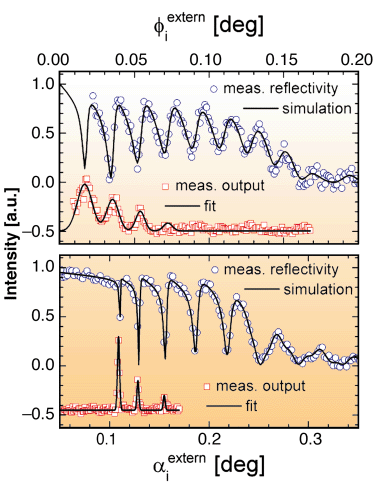
Experimentally, the resonant waveguide effects were evidenced in several ways: (i) The measured reflectivity curves of the nanostructure both as a function of  i (
i ( i = const.,
i = const.,  f = 2
f = 2 i) and
i) and  i (
i ( i = const.,
i = const.,  f = 2
f = 2 i) show the characteristic cusps, see Figure 121. Waveguide effects readily manifest themselves in the reflectivity curve as cusps in the plateau of otherwise total external reflection. (ii) The far field pattern of the lowest lying mode was measured with a high-resolution CCD camera and showed the expected distribution. (iii) The excitation characteristics were measured, i.e. the integrated far-field intensity was measured in a mesh scan of (
i) show the characteristic cusps, see Figure 121. Waveguide effects readily manifest themselves in the reflectivity curve as cusps in the plateau of otherwise total external reflection. (ii) The far field pattern of the lowest lying mode was measured with a high-resolution CCD camera and showed the expected distribution. (iii) The excitation characteristics were measured, i.e. the integrated far-field intensity was measured in a mesh scan of ( i/
i/  i ). (iv) Additionally, the 'point source' character of the recorded beam was evidenced by translating a knife-edge in the divergent waveguide beam, resulting in the geometrically expected cross-section.
i ). (iv) Additionally, the 'point source' character of the recorded beam was evidenced by translating a knife-edge in the divergent waveguide beam, resulting in the geometrically expected cross-section.
 |
|
|
Possible future applications of 2D X-ray waveguides include phase-contrast projection microscopy, as already demonstrated in the case of the 1D counterpart [3]. Apart from microscopy and imaging, all conventional X-ray applications that would benefit from coherent beams of sub-micrometre cross-sections, can be addressed, in the field of imaging, scattering and photon correlation spectroscopy.
References
[1] Y.P. Feng et al., Phys. Rev. Lett. 71, 537 (1993), M.J. Zwanenburg et al., Phys.Rev.Lett. 82, 1696 (1999).
[2] F. Pfeiffer, T. Salditt, P. Høghøj and I. Anderson, SPIE Proceedings 4145, (2001).
[3] S. Lagomarsino, A. Cedola, P. Cloetens, et al., Appl. Phys. Lett. 71, No. 18 (1997).
Principal Publications and Authors
F. Pfeiffer (a), C. David (b), M. Burghammer (c), C. Riekel (c), and T. Salditt (a,d), Science 297, 230 (2002).
(a) Universität Saarbrücken (Germany)
(b) Paul-Scherrer Institut Villingen (Switzerland)
(c) ESRF
(d) now at: Institut für Röntgenphysik, Universität Göttingen (Germany)



