- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2002
- High Resolution and Resonance Scattering
- Phonon Dispersion in the New Superconductor MgB2
Phonon Dispersion in the New Superconductor MgB2
The discovery of 39 K superconductivity in MgB2 [1] has led to in-depth study of the material and a picture has emerged of a phonon-mediated superconductor described by conventional theory, in contrast to high-temperature superconductors. The unusually high transition temperature mainly finds a justification in the high energy vibrational modes of the light B atoms. Additional peculiarities of this material, such as strong electron-phonon coupling (EPC) and anharmonicity, have been noted by various authors. Measurement of phonon dispersion and the evolution of phonon lifetimes over the Brillouin Zone (BZ) would shed more light on these aspects but has been impeded by the absence of large single crystals. This problem was circumvented by the use of inelastic X-ray scattering of a focused and intense X-ray beam at ID28. This technique is now routinely used in small (~100 µm) single crystalline samples and is well adapted for the measurement of high-energy optical modes. In this work we present the first measured phonon dispersion curves and linewidths in MgB2 along three major directions in the BZ,  -A,
-A,  -M and A-L and at a temperature of 300K. We also calculate phonon dispersion and the contributions of EPC and anharmonicity to the linewidth using Density Functional Theory in the generalised gradient approximation.
-M and A-L and at a temperature of 300K. We also calculate phonon dispersion and the contributions of EPC and anharmonicity to the linewidth using Density Functional Theory in the generalised gradient approximation.
 |
|
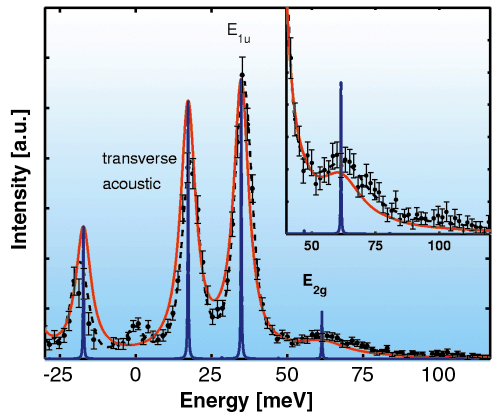
Fig. 67: Energy loss scan in almost transverse geometry measured at 0.6 |
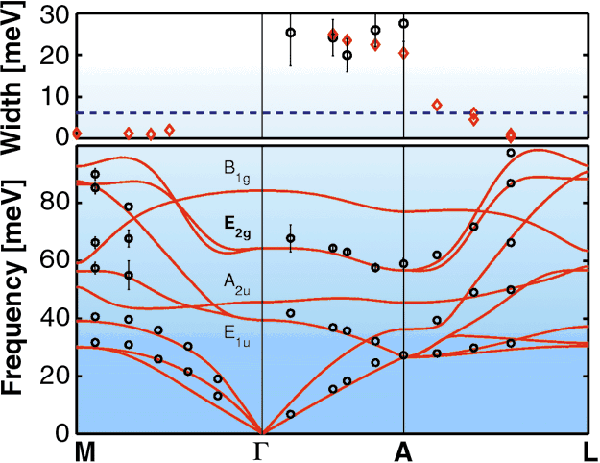
Figure 67 shows the energy loss scan at 0.6  -A. The acoustic mode as well as the lower energy E1u optical mode are visible as resolution-limited (6.1 meV FWHM) peaks. Most importantly, a broad peak is observed at higher energy loss, corresponding to the E2g optical mode in which the B atoms vibrate in-plane in opposite directions while the Mg atoms are stationary. By measuring similar energy loss scans over three directions in the BZ and extracting the linewidth of the E2g mode where possible, we map the phonon dispersion of all modes and the E2g linewidth variation shown in Figure 68. Also shown is the theoretical dispersion. Calculated structure factors and energies show excellent quantitative agreement with our measured data. The measured as well as calculated linewidth of the E2g branch, shown in the top panel of Figure 68, is strongly anisotropic in the BZ. Along
-A. The acoustic mode as well as the lower energy E1u optical mode are visible as resolution-limited (6.1 meV FWHM) peaks. Most importantly, a broad peak is observed at higher energy loss, corresponding to the E2g optical mode in which the B atoms vibrate in-plane in opposite directions while the Mg atoms are stationary. By measuring similar energy loss scans over three directions in the BZ and extracting the linewidth of the E2g mode where possible, we map the phonon dispersion of all modes and the E2g linewidth variation shown in Figure 68. Also shown is the theoretical dispersion. Calculated structure factors and energies show excellent quantitative agreement with our measured data. The measured as well as calculated linewidth of the E2g branch, shown in the top panel of Figure 68, is strongly anisotropic in the BZ. Along  -A it is particularly large signifying short lifetimes or heavy damping. In the other directions the linewidth is more difficult to extract due to unfavourable structure factor or overlap with other modes. However, we could determine that near the M and L points it is below the experimental resolution, i.e. at least 5 times smaller than along
-A it is particularly large signifying short lifetimes or heavy damping. In the other directions the linewidth is more difficult to extract due to unfavourable structure factor or overlap with other modes. However, we could determine that near the M and L points it is below the experimental resolution, i.e. at least 5 times smaller than along  -A. This is also borne out by calculations which further attribute the damping almost excusively to EPC (the contribution shown in Figure 68) since the anharmonic contribution is much smaller.
-A. This is also borne out by calculations which further attribute the damping almost excusively to EPC (the contribution shown in Figure 68) since the anharmonic contribution is much smaller.
 |
|
Fig. 68: (Bottom) Experimental (circles) and theoretical phonon dispersion (red line). The optical modes are labelled according to the symmetry at the |
In conclusion we have shown that the E2g optical mode is strongly damped in certain regions of the Brillouin Zone in MgB2. Calculations attribute this behaviour exclusively to electron-phonon coupling as a consequence of Fermi surface nesting. In MgB2 this points to the possibility of directly determining the contribution of this mode to electron-phonon coupling from the measured linewidth.
References
[1] J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani, and J. Akimitsu, Nature 410, 63 (2001).
Principal Publication and Authors
A. Shukla (a), M. Calandra (a), M. d'Astuto (b), M. Lazzeri (a), F. Mauri (a), C. Bellin (a), M. Krisch (b), J. Karpinski (c), S.M. Kazakov (c), J. Jun (c), D. Daghero (d), and K. Parlinski (e), Phys. Rev. Lett. (cond-mat/0209064), accepted (2003).
(a) LMCP, Université Pierre et Marie Curie, Paris (France)
(b) ESRF
(c) Solid state Physics Laboratory, ETH, Zürich (Switzerland)
(d) INFM-Dipartimento di Fisica, Politecnico di Torino (Italy)
(e) Institute of Nuclear Physics, Cracow (Poland)



