- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2002
- High Resolution and Resonance Scattering
- Deep Inelastic Atomic Scattering of X-rays in Liquid Neon
Deep Inelastic Atomic Scattering of X-rays in Liquid Neon
Deep inelastic scattering experiments are used in many research areas of physics and are based on the following argument. If the energy, E, and the momentum, q, which are transferred in a scattering experiment from the probe particle to the target particle are very high compared to the characteristic energy and momentum of the target particle, the latter can be considered to recoil freely from the collision, and the scattered probe particle carries information on the initial momentum distribution of the target particles. If the probe is an X-ray beam, the natural deep inelastic scattering regime is the usual Compton limit where the electronic momentum distribution is experimentally accessed. The low energy part of the spectrum of the scattered X-rays reflects - via the adiabatic approximation - the atomic dynamics. The question to be addressed here is whether it is possible to select an appropriate energy and momentum transfer range where the scattering of X-rays can also be used to obtain information on the atomic momentum distribution, which to date was only accessed in high-q neutron scattering experiments.
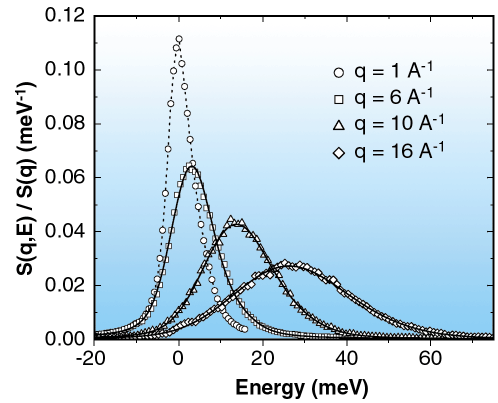
The experiment has been carried out at beamline ID16 using the vertical arm spectrometer for the scattered energy analysis with an instrumental energy resolution of 6.9 meV (FWHM). Inelastic X-ray scattering spectra of liquid Neon were collected for several q values between 1.0 and 16.0 Å1. The sample was kept at a temperature of 27.6 ± 0.1 K and at a pressure of 1.4 ± 0.2 bar. The spectral intensities (Figure 73) appear as structureless peaks that, with increasing q, shift towards higher energies and broaden. On approaching the impulse approximation regime, the dynamic structure factor S(q,E) (proportional to the inelastic X-ray scattering cross-section) is expected to shift in energy as q2 and to broaden as q. The spectra in Figure 73 do present such behaviour, and this shows that the impulse approximation regime is being reached. Clearly, the impulse approximation regime found here corresponds to the scattering of the X-rays from the neon core electrons with an effective mass given by the atomic mass.
 |
|
Fig. 73: Normalised spectral intensities of liquid neon at selected values of the exchanged momentum, q. The full lines correspond to the additive approach model of Ref. [1]; the dashed line superimposed on the q = 1 Å1 spectrum is a guide for the eye. |
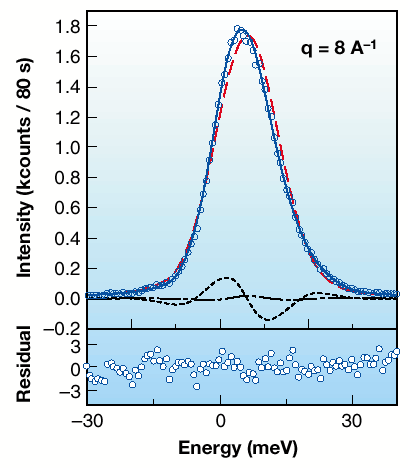
For a quantitative description of the spectra, the so-called additive approach model [1] has been followed here, which amounts in approximating the dynamic structure factor as the sum of a dominant Gaussian contribution to describe the momentum distribution plus corrective terms to describe the final state effects. These latter effects are due to the fact that the impulse approximation is reached only asymptotically: the struck atom cannot be considered to recoil completely freely from the collision, and the effects coming from the interaction of the struck atom with the neighbouring atoms have to be taken into account. On adjusting this model to the experimental data (Figure 73 and Figure 74) it is possible to determine quantities as the mean atomic kinetic energy which, for this moderately quantum liquid, comes out to be Ek = 51 ± 3 K, in agreement with neutron scattering determinations [2]. This shows that deep inelastic atomic scattering of X-rays is indeed achievable, which might be of particular interest in cases as that of 3He, a system of broad interest but irksome for neutron scattering due to its large absorption.
 |
|
Fig. 74: Upper part: the spectrum of liquid neon at q = 8 Å1 is reported together with the best fit of the model of Ref. [1] to the data (full line). Here, the model line is the sum of three contributions: a dominant Gaussian contribution (dashed red line) and two correction terms (dashed and dotted-dashed black lines). Bottom part: Residuals of the fit, in standard deviation units. |
References
[1] H.R. Glyde, Phys. Rev. B 50, 6726-6742 (1994).
[2] R.T. Azuah, W.G. Stirling, H.R. Glyde, P.E. Sokol, S.M. Bennington, Phys. Rev. B 51, 605-608 (1995).
Principal Publication and Authors
G. Monaco (a), A. Cunsolo (b), G. Pratesi (c), F. Sette (a), R. Verbeni (a), Phys. Rev. Lett. 88, 227401 (2002).
(a) ESRF
(b) Universita' di Roma Tre, Rome (Italy)
(c) Universita' di Firenze, Florence (Italy)



