- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2001
- Surfaces, Interfaces and Nano-science
- Strain and Stacking of GaN Quantum Dots in Multilayers
Strain and Stacking of GaN Quantum Dots in Multilayers
The current interest in self-organised growth of strained semiconductor nano-structures is based on the possibility of achieving novel optical and electronic properties. Among them, nitride compounds are especially interesting due to their application in the blue-ultraviolet wavelength range. In the system GaN/AlN (wurtzite phase), the in-plane lattice mismatch amounts to 2.4%. The resulting strain, which accumulates during the molecular beam epitaxy of GaN on AlN induces the Stranski-Krastanov transition from a 2D layer-by-layer growth to a 3D growth of dislocation-free islands. Embedded in the AlN matrix, these GaN islands behave like artificial atoms and are called quantum dots.
The electronic properties of the quantum dots are considerably influenced by their internal structure. It has been shown that the growth of quantum dots in superlattices results in an improved size distribution and a good vertical stacking. These properties, which are difficult to observe with real space methods can be obtained by X-rays, where the information is averaged over a macroscopic ensemble of the dots. Since the total thickness of the superlattice is typically only some tens of nm thick, grazing-incidence X-ray scattering using synchrotron radiation allows us to study strain and ordering of the quantum dots, even as a function of depth. The GaN quantum dot multilayer samples are grown in a commercial MECA 2000 MBE chamber. The multilayer, consisting of 13 GaN/AlN bi-layers with a AlN spacer layer thickness of 4 nm, was deposited on a SiC (0001) substrate (Figure 70a).
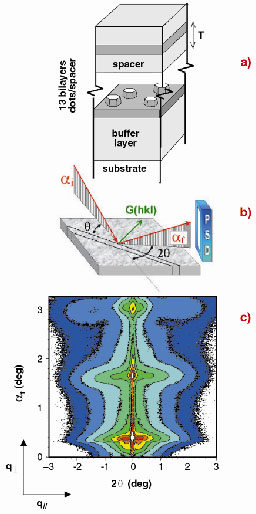 |
Fig. 70: (a) Sample; (b) Set-up used for grazing-incidence scattering methods; (c) GISAXS pattern showing Bragg sheets of diffuse intensity. |
The X-ray grazing incidence (GI) experiments have been performed at beamline ID1. The intensity is collected with a linear detector as a function of the angle 2, measured from the plane of incidence (Figure 70b). The corresponding q
and q// reciprocal space axis are aligned normal and parallel to the surface plane, respectively. In the grazing-incidence small-angle X-ray scattering regime (GISAXS), for small 2
values, the scattered intensity is governed by the morphological properties of the dot multilayer. In the grazing-incidence diffraction (GID) regime, at large 2
values, the surface Bragg peaks are exploited to measure the strain distribution in the superlattice. The variation of the incidence angle ai allows depth sensitive measurements.
The reciprocal space intensity map, representing the GISAXS pattern, is shown in Figure 70c. Three intense Bragg sheets indicate the high replication of the quantum dots in vertical stacks. They permit the quantification of the degree of vertical ordering [1]. We find that the dots throughout the whole superlattice deviate from an average stack position by only about 4% of their diameter of 15 nm. From other quantum dot systems it is known that the vertical ordering is mediated by strain, which here has been measured by GID (Figure 71) performing radial scans close to a (30-30) surface reflection. We observed that the lateral lattice parameter distribution induces two maxima (apart from the sharp SiC substrate peak) which can be attributed to the undistorted part of the AlN superlattice and buffer layer and a broad peak (noted (A) and (B)) resulting from GaN quantum dots strained to a lattice parameter smaller than the bulk value of GaN. The green curve stems from a scattering depth of roughly 10 nm while the blue one represents the whole multilayer. The shift of the GaN peak from position (A) to (B) evidences an increase of lattice relaxation near the sample surface [2].
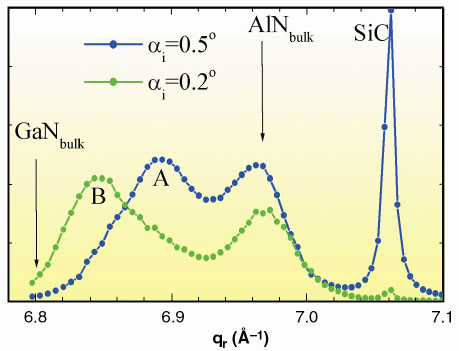 |
Fig. 71: GID scans in radial direction qr at the (30-30) Bragg reflection for different |
To conclude, we have shown that GISAXS and GID are well-suited techniques to quantify strain and ordering of self-assembled nanostructures in group III nitrides. The systematic investigation of samples with varying spacer layer thickness is underway and aims to improve our understanding of the growth mechanisms in this QD system.
References
[1] I. Kegel, T.H. Metzger, J. Peisl, J. Stangl, G. Bauer and D. Smilgies, Phys. Rev. B 60, 2516 (1999).
[2] V. Chamard, T.H. Metzger, and E. Bellet-Amalric, B. Daudin, C. Adelmann, H. Mariette and G. Mula, Appl. Phys. Lett., 79, 1971 (2001).
Authors:
V. Chamard (a), T. Metzger (a), E. Bellet-Almaric (b), B. Daudin (b), H. Mariette (b, c) and C. Adelmann (b)
(a) ESRF
(b) Département de Recherche Fondamentale sur la Matière Condensée, CEA/Grenoble (France)
(c) Laboratoire de Spectrométrie Physique, Université J. Fourier Grenoble 1 - CNRS UMR 5588, Saint Martin d'Hères (France)



