- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Soft Condensed Matter
- Correlation Spectroscopy on Filled Polymers and their Flocculation
Correlation Spectroscopy on Filled Polymers and their Flocculation
Blending fillers into a rubber increases its mechanical strength. Such fillers generally consist of small (5-100 nm) primary particles (carbon black or silica) bonded together in rigid aggregates. Optimum mechanical results are achieved when the aggregates percolate throughout the specimen. Sometimes, however, aggregates migrate inside the rubber to form coarser, weakly bound clusters called agglomerates, a process known as flocculation. In an automobile tyre, flocculation means higher energy losses and greater fuel consumption.
To investigate this process, pyrogenic silica blended into a molten polymer (polydimethyl siloxane) of low molecular weight was investigated at the CRG beamline BM2 using coherent X-ray spectroscopy. Depending on whether or not hydrophobic surface treatment was previously applied to the silica, these mixtures are either viscous liquids (sample 1) or thixotropic (sample 2). For a given wave vector q, the correlation function G(q,t) describing the changes in time of the speckle pattern of photons scattered by the filler is
![]() (1)
(1)
where ß is an apparatus constant and ![]() is governed by the rate of diffusion D of the particles moving in the sample,
is governed by the rate of diffusion D of the particles moving in the sample,
![]() = Dq2 (2)
= Dq2 (2)
Figure 45 shows X-ray intensity correlation functions of three samples at the same value of q. In the dry powder the particles are stationary and G(q,t) is a constant. For sample 1, however, G(q,t) relaxes in about a hundred seconds. In sample 2 the decay rate ![]() is slower.
is slower.
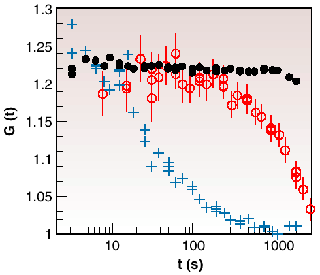 |
Fig. 45: X-ray intensity correlation functions at q = 1.71 10 -2 nm -1 for: (
|
In both suspensions, mechanical stirring disrupts the agglomerates, but since these recombine at a rate 1/![]() f, expression (2) should be replaced by
f, expression (2) should be replaced by
![]() = Dq2 [1+ a exp(t0 /
= Dq2 [1+ a exp(t0 / ![]() f)] (3)
f)] (3)
where (1+a ) is the ratio of size of the agglomerate to that of its component fragments and t0 is the time elapsed after stirring.
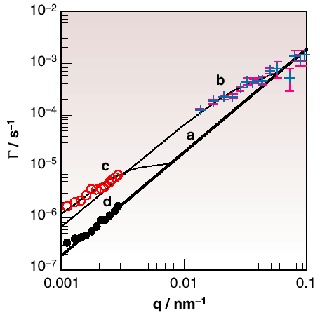 |
Fig. 46:
|
Figure 46 shows ![]() (q) for sample 2, measured by coherent SAXS and also by small-angle light scattering (SALS). For large t0and q, the data collapse on the asymptotic line as defined by eq. 2. In each sample, however, the data at short times t0 or small q lie above the asymptotic line, showing that mechanical mixing breaks the agglomerates into smaller units. The thin lines in Figure 46 passing through the data points b (t0 = 104 s; coherent SAXS) and c (t0 = 7 105 s; SALS) are fits to eq. 3. Consistency with the results, however, requires that
(q) for sample 2, measured by coherent SAXS and also by small-angle light scattering (SALS). For large t0and q, the data collapse on the asymptotic line as defined by eq. 2. In each sample, however, the data at short times t0 or small q lie above the asymptotic line, showing that mechanical mixing breaks the agglomerates into smaller units. The thin lines in Figure 46 passing through the data points b (t0 = 104 s; coherent SAXS) and c (t0 = 7 105 s; SALS) are fits to eq. 3. Consistency with the results, however, requires that
1/![]() f = Dfq2 (4)
f = Dfq2 (4)
where Df is a constant. The unperturbed translational diffusion coefficients D are 5 10-14 cm2s-1 (sample 1) and 2 10-15 cm2s-1 (sample 2). The flocculation process is even slower: Df = 2 10-15 cm2s-1 (sample 1) and 9 10-16 cm2s-1 (sample 2). These results demonstrate that flocculation in this system is governed by a diffusion mechanism. To measure such effects on a macroscopic scale (e.g. 1 mm) would require many thousands of years; coherent X-ray spectroscopy greatly shortens the measurement time.
Principal Publication and Authors
E. Geissler (a), A-M. Hecht (a), C. Rochas (a), F. Bley (b), F. Livet (b) and M. Sutton (a,c), Phys. Rev. E, 62, 8308 (2000).
(a) LSP, CNRS-HJF, Grenoble (France)
(b) LTPCM, INPG, Grenoble (France)
(c) McGill University, Montreal (Canada)



